JackCin's blog
JackCin
2023-09-13
目录

数组

# 数组

  • 数组是存放在连续内存空间上的相同类型数据的集合。

数组可以方便的通过下标索引的方式获取到下标下对应的数据。

举一个字符数组的例子，如图所示：

算法通关数组

  • 需要两点注意的是

    • 数组下标都是从0开始的。

    • 数组内存空间的地址是连续的

  • 正是因为数组的在内存空间的地址是连续的，所以我们在删除或者增添元素的时候，就难免要移动其他元素的地址。

例如删除下标为3的元素，需要对下标为3的元素后面的所有元素都要做移动操作，如图所示：

算法通关数组1

  • 而且大家如果使用C++的话，要注意vector 和 array的区别，vector的底层实现是array，严格来讲vector是容器，不是数组。

  • 数组的元素是不能删的，只能覆盖。

那么二维数组直接上图，大家应该就知道怎么回事了

算法通关数组2

那么二维数组在内存的空间地址是连续的么？

不同编程语言的内存管理是不一样的，以C++为例，在C++中二维数组是连续分布的。

我们来做一个实验，C++测试代码如下：

void test_arr() {
    int array[2][3] = {
		{0, 1, 2},
		{3, 4, 5}
    };
    cout << &array[0][0] << " " << &array[0][1] << " " << &array[0][2] << endl;
    cout << &array[1][0] << " " << &array[1][1] << " " << &array[1][2] << endl;
}

int main() {
    test_arr();
}
1
2
3
4
5
6
7
8
9
10
11
12

测试地址为

0x7ffee4065820 0x7ffee4065824 0x7ffee4065828
0x7ffee406582c 0x7ffee4065830 0x7ffee4065834
1
2

注意地址为16进制，可以看出二维数组地址是连续一条线的。

一些录友可能看不懂内存地址，我就简单介绍一下， 0x7ffee4065820 与 0x7ffee4065824 差了一个4，就是4个字节，因为这是一个int型的数组，所以两个相邻数组元素地址差4个字节。

0x7ffee4065828 与 0x7ffee406582c 也是差了4个字节，在16进制里8 + 4 = c，c就是12。

如图：

数组内存

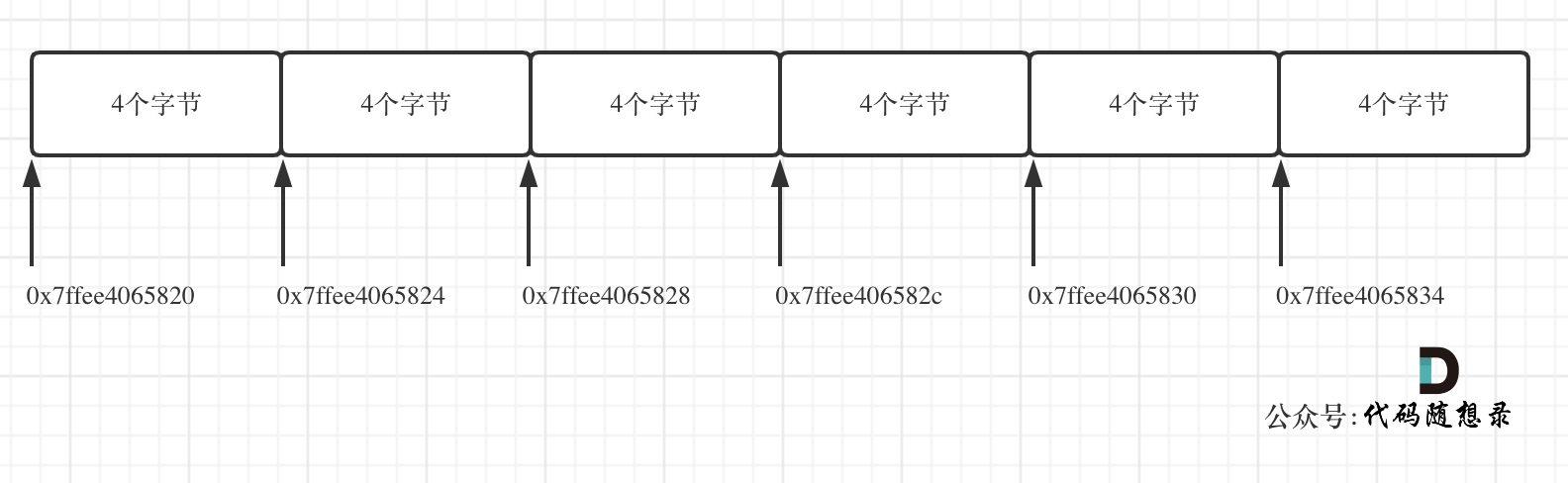
所以可以看出在C++中二维数组在地址空间上是连续的。

像Java是没有指针的，同时也不对程序员暴露其元素的地址，寻址操作完全交给虚拟机。

所以看不到每个元素的地址情况，这里我以Java为例，也做一个实验。

public static void test_arr() {
    int[][] arr = {{1, 2, 3}, {3, 4, 5}, {6, 7, 8}, {9,9,9}};
    System.out.println(arr[0]);
    System.out.println(arr[1]);
    System.out.println(arr[2]);
    System.out.println(arr[3]);
}
1
2
3
4
5
6
7

输出的地址为：

[I@7852e922
[I@4e25154f
[I@70dea4e
[I@5c647e05
1
2
3
4

这里的数值也是16进制，这不是真正的地址，而是经过处理过后的数值了，我们也可以看出，二维数组的每一行头结点的地址是没有规则的，更谈不上连续。

所以Java的二维数组可能是如下排列的方式：

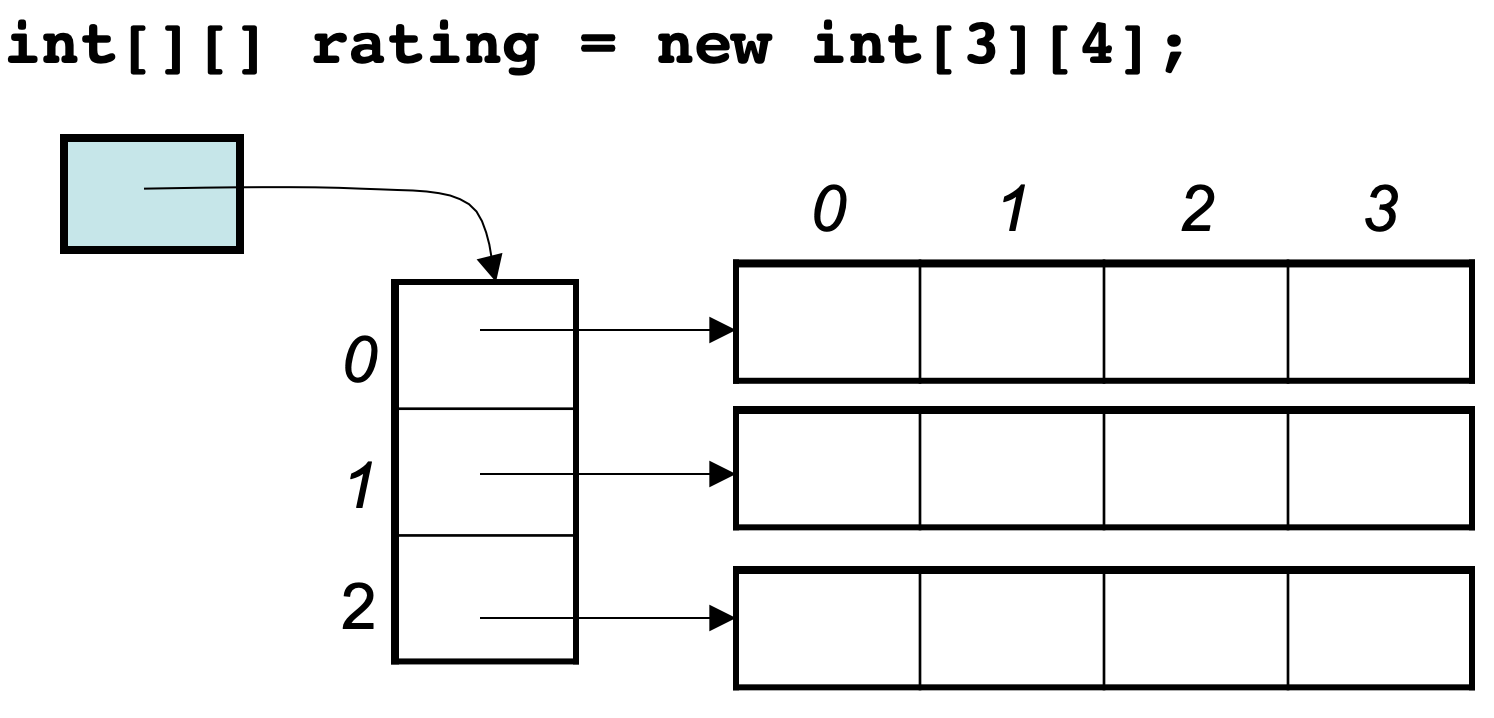
算法通关数组3

# 二分查找

  • 细节分析
    • 1、判断区间，（左闭右闭 / 左闭右开）
    • 2、right值在左闭右开时应为数组长度，左闭右闭时为数组长度减1；
    • 3、while（）循环里注意left是否可以等于right，左闭右闭（==），左闭右开（!=）
    • 4、middle防止 left+right 溢出，最好写成 left + ( right - left) / 2

# 一、二分查找

力扣题目链接 (opens new window)

# 题目

  • 给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

  • 示例1：

    输入: nums = [-1,0,3,5,9,12], target = 9     
输出: 4       
解释: 9 出现在 nums 中并且下标为 4
    1
    2
    3

  • 示例2：

    输入: nums = [-1,0,3,5,9,12], target = 2     
输出: -1        
解释: 2 不存在 nums 中因此返回 -1
    1
    2
    3

提示：

  • 你可以假设 nums 中的所有元素是不重复的。
  • n 将在 [1, 10000]之间。
  • nums 的每个元素都将在 [-9999, 9999]之间

# 思路

  • 这道题目的前提是数组为有序数组，同时题目还强调数组中无重复元素，因为一旦有重复元素，使用二分查找法返回的元素下标可能不是唯一的，这些都是使用二分法的前提条件，当大家看到题目描述满足如上条件的时候，可要想一想是不是可以用二分法了。
  • 二分查找涉及的很多的边界条件，逻辑比较简单，但就是写不好。例如到底是 while(left < right) 还是 while(left <= right)，到底是right = middle呢，还是要right = middle - 1呢？
  • 大家写二分法经常写乱，主要是因为对区间的定义没有想清楚，区间的定义就是不变量。要在二分查找的过程中，保持不变量，就是在while寻找中每一次边界的处理都要坚持根据区间的定义来操作，这就是循环不变量规则。
  • 写二分法，区间的定义一般为两种，左闭右闭即[left, right]，或者左闭右开即[left, right)。
  • 下面用这两种区间的定义分别讲解两种不同的二分写法。

# 1、左闭右闭

第一种写法，我们定义 target 是在一个在左闭右闭的区间里，也就是[left, right] （这个很重要非常重要）。

区间的定义这就决定了二分法的代码应该如何写，因为定义target在[left, right]区间，所以有如下两点：

  • while (left <= right) 要使用 <= ，因为left == right是有意义的，所以使用 <=
  • if (nums[middle] > target) right 要赋值为 middle - 1>，因为当前这个nums[middle]一定不是target，那么接下来要查找的左区间结束下标位置就是 middle - 1

例如在数组：1,2,3,4,7,9,10中查找元素2，如图所示：

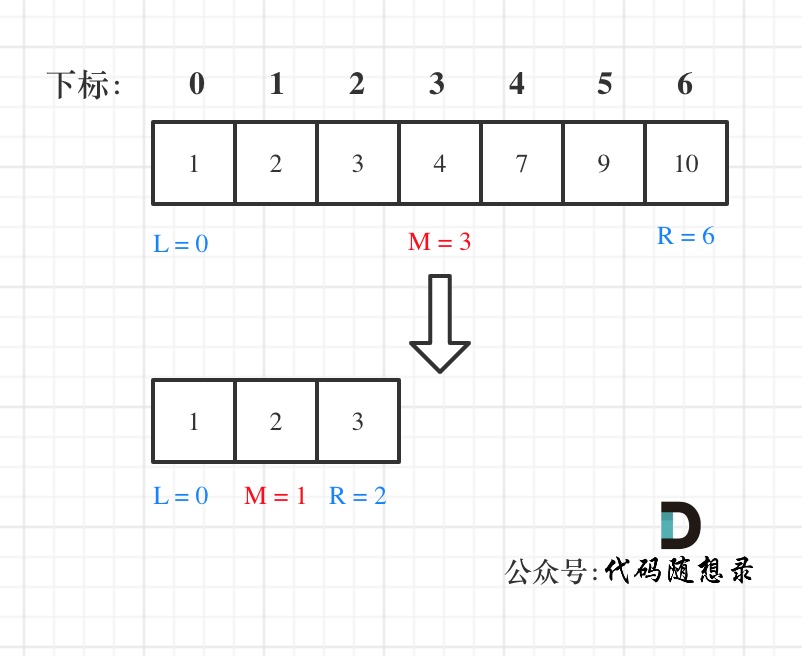
704.二分查找

// (版本一) 左闭右闭区间 [left, right]
int search(int* nums, int numsSize, int target){
    int left = 0;
    int right = numsSize-1;
    int middle = 0;
    //若left小于等于right，说明区间中元素不为0
    while(left<=right) {
        //更新查找下标middle的值
        middle = (left+right)/2;
        //此时target可能会在[left,middle-1]区间中
        if(nums[middle] > target) {
            right = middle-1;
        } 
        //此时target可能会在[middle+1,right]区间中
        else if(nums[middle] < target) {
            left = middle+1;
        } 
        //当前下标元素等于target值时，返回middle
        else if(nums[middle] == target){
            return middle;
        }
    }
    //若未找到target元素，返回-1
    return -1;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

# 2、左闭右开

如果说定义 target 是在一个在左闭右开的区间里，也就是[left, right) ，那么二分法的边界处理方式则截然不同。

有如下两点：

  • while (left < right)，这里使用 < ,因为left == right在区间[left, right)是没有意义的
  • if (nums[middle] > target) right 更新为 middle，因为当前nums[middle]不等于target，去左区间继续寻找，而寻找区间是左闭右开区间，所以right更新为middle，即：下一个查询区间不会去比较nums[middle]

在数组：1,2,3,4,7,9,10中查找元素2，如图所示：（注意和方法一的区别）

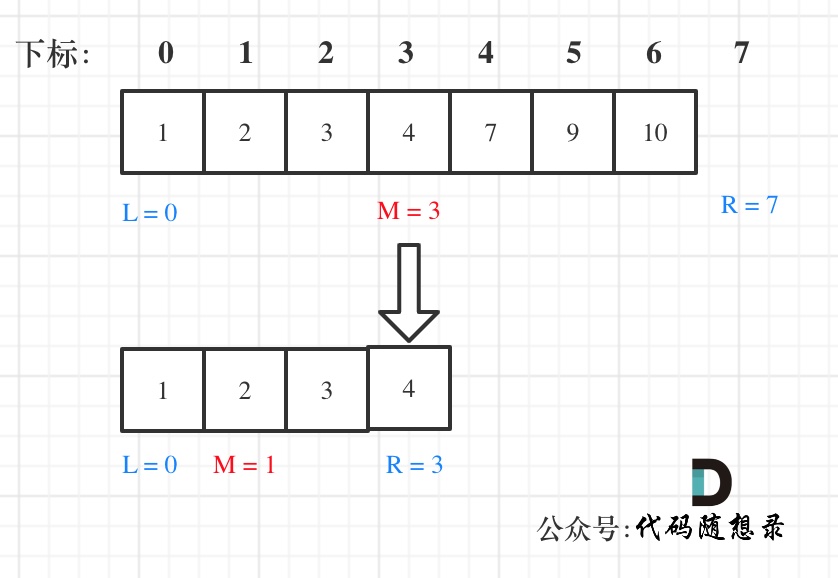
704.二分查找1

代码如下：（详细注释）

// (版本二) 左闭右开区间 [left, right)
int search(int* nums, int numsSize, int target){
    int length = numsSize;
    int left = 0;
    int right = length;	//定义target在左闭右开的区间里，即：[left, right)
    int middle = 0;
    while(left < right){  // left == right时，区间[left, right)属于空集，所以用 < 避免该情况
        int middle = left + (right - left) / 2;
        if(nums[middle] < target){
            //target位于(middle , right) 中为保证集合区间的左闭右开性，可等价为[middle + 1,right)
            left = middle + 1;
        }else if(nums[middle] > target){
            //target位于[left, middle)中
            right = middle ;
        }else{	// nums[middle] == target ，找到目标值target
            return middle;
        }
    }
    //未找到目标值，返回-1
    return -1;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
  • 时间复杂度：O(log n)
  • 空间复杂度：O(1)

# 二、搜索插入位置

力扣题目链接 (opens new window)

# 题目

  • 给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

# 思路

# 1、左闭右闭

  • 以这道题目来举例，以下的代码中定义 target 是在一个在左闭右闭的区间里，也就是[left, right] （这个很重要）。
  • 这就决定了这个二分法的代码如何去写，大家看如下代码：
  • 大家要仔细看注释，思考为什么要写while(left <= right)， 为什么要写right = middle - 1。
//版本一 [left, right]左闭右闭区间
int searchInsert(int* nums, int numsSize, int target){
    //左闭右开区间 [0 , numsSize-1]
        int left =0;
        int mid =0;
        int right = numsSize - 1;
        while(left <= right){//左闭右闭区间 所以可以 left == right
            mid = left + (right - left) / 2;
            if(target < nums[mid]){
        //target 在左区间 [left, mid - 1]中，原区间包含mid，右区间边界可以向左内缩
                right = mid -1;
            }else if( target > nums[mid]){
        //target 在右区间 [mid + 1, right]中,原区间包含mid，左区间边界可以向右内缩
                left = mid + 1;
            }else {
        // nums[mid] == target ，顺利找到target，直接返回mid
                return mid;
            }
        }
        // 分别处理如下四种情况
        // 目标值在数组所有元素之前  [0, -1]
        // 目标值等于数组中某一个元素  return middle;
        // 目标值插入数组中的位置 [left, right]，return  right + 1
        // 目标值在数组所有元素之后的情况 [left, right]， 因为是右闭区间，所以 return right + 1
        return right + 1;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
  • 时间复杂度：O(log n)
  • 空间复杂度：O(1)

# 2、左闭右开

  • 如果说定义 target 是在一个在左闭右开的区间里，也就是[left, right) 。
  • 那么二分法的边界处理方式则截然不同。
  • 不变量是[left, right)的区间，如下代码可以看出是如何在循环中坚持不变量的。
  • 大家要仔细看注释，思考为什么要写while (left < right)， 为什么要写right = middle。
//版本二 [left, right]左闭右开区间
int searchInsert(int* nums, int numsSize, int target){
    //左闭右开区间 [0 , numsSize)
        int left =0;
        int mid =0;
        int right = numsSize;
        while(left < right){//左闭右闭区间 所以 left < right
            mid = left + (right - left) / 2;
            if(target < nums[mid]){
        //target 在左区间 [left, mid)中，原区间没有包含mid，右区间边界不能内缩
                right = mid ;
            }else if( target > nums[mid]){
        // target 在右区间 [mid+1, right)中，原区间包含mid，左区间边界可以向右内缩
                left = mid + 1;
            }else {
        // nums[mid] == target ，顺利找到target，直接返回mid
                return mid;
            }
        }
		 // 分别处理如下四种情况
        // 目标值在数组所有元素之前 [0,0)
        // 目标值等于数组中某一个元素 return middle
        // 目标值插入数组中的位置 [left, right) ，return right 即可
        // 目标值在数组所有元素之后的情况 [left, right)，因为是右开区间，所以 return right
        return right;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

# 三、查找元素范围

力扣链接 (opens new window)

# 题目

  • 给定一个按照升序排列的整数数组 nums，和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。
  • 如果数组中不存在目标值 target，返回 [-1, -1]。
  • 进阶：你可以设计并实现时间复杂度为 $O(\log n)$ 的算法解决此问题吗？

# 思路

  • 下面我来把所有情况都讨论一下。

    寻找target在数组里的左右边界，有如下三种情况：

    • 情况一：target 在数组范围的右边或者左边，例如数组{3, 4, 5}，target为2或者数组{3, 4, 5},target为6，此时应该返回{-1, -1}
    • 情况二：target 在数组范围中，且数组中不存在target，例如数组{3,6,7},target为5，此时应该返回{-1, -1}
    • 情况三：target 在数组范围中，且数组中存在target，例如数组{3,6,7},target为6，此时应该返回{1, 1}

    这三种情况都考虑到，说明就想的很清楚了。

    接下来，在去寻找左边界，和右边界了。

# 1、寻找左边界

//获取左边界
int getLeftBorder(int* nums, int numsSize, int target){
    int left = 0;
    int right = numsSize-1;
    int middle =0;
    int leftBorder =-2;  //记录一下rightBorder没有被赋值的情况
    while(left<=right){
        middle = left + (( right - left ) / 2);   //防止 right + left后溢出
        // middle= (left + right)/2;
        if(nums[middle] < target){
            left= middle + 1;
        }
        // 寻找左边界，就要在nums[middle] >= target的时候更新right
        else {
            right = middle-1;
            leftBorder = right;
        }
    }
    return leftBorder;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

# 2、寻找右边界

 //先获取右边界
int getRightBorder(int* nums, int numsSize, int target){
    int left = 0;
    int right = numsSize-1;  //记得减一
    int middle =0;
    int rightBorder =-2;  //记录一下rightBorder没有被赋值的情况
    while(left<=right){
        middle=left + (( right - left ) / 2);
         // 寻找右边界，就要在nums[middle] <= target的时候更新left
        if(nums[middle] <= target){  
            left= middle + 1;
            rightBorder =left;
        }
        else {
            right= middle-1;
        }c
    }
    return rightBorder;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

# 3、判断情况

//这里定义为int指针，所以返回值也必须是int指针
int* searchRange(int* nums, int numsSize, int target, int* returnSize){
    //力扣里面c代码给的函数里这个returnSize是来指明返回值大小的
     *returnSize = 2;
    int rightBorder = getRightBorder(nums, numsSize,target);
    int leftBorder = getLeftBorder(nums, numsSize,target);
    //给指针分配空间
    int *arr=(int*)malloc(sizeof(int)*2);
    //如果两个边界中有一个没被赋过值，就说明它是小于或大于数组中的数的
    if(rightBorder == -2 || leftBorder == -2){
        arr[0] = -1;
        arr[1] = -1;
        return arr;
    }
    //left和right相等后还会再执行一次循环，会导致边界再多移动一次，所以LB要加1，RB要减1
    if(rightBorder - leftBorder > 1){
         arr[0] = leftBorder + 1;
        arr[1] =  rightBorder - 1;
        return arr;
    }
    //剩下就是target数组大小范围再数组中，但是数组无这个数
        arr[0] = -1;
        arr[1] = -1;
        return arr;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

# 更多二分解法：

class Solution {
    public int[] searchRange(int[] nums, int target) {
        int[] res = new int[] {-1, -1};
        res[0] = binarySearch(nums, target, true);
        res[1] = binarySearch(nums, target, false);
        return res;
    }
    //leftOrRight为true找左边界 false找右边界
    public int binarySearch(int[] nums, int target, boolean leftOrRight) {
        int res = -1;
        int left = 0, right = nums.length - 1, mid;
        while(left <= right) {
            mid = left + (right - left) / 2;
            if(target < nums[mid])
                right = mid - 1;
            else if(target > nums[mid])
                left = mid + 1;
            else {
                res = mid;
                //处理target == nums[mid]
                if(leftOrRight)
                    right = mid - 1;
                else
                    left = mid + 1;
            }
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
// 解法2
// 1、首先，在 nums 数组中二分查找 target；
// 2、如果二分查找失败，则 binarySearch 返回 -1，表明 nums 中没有 target。此时，searchRange 直接返回 {-1, -1}；
// 3、如果二分查找成功，则 binarySearch 返回 nums 中值为 target 的一个下标。然后，通过左右滑动指针，来找到符合题意的区间

class Solution {
	public int[] searchRange(int[] nums, int target) {
		int index = binarySearch(nums, target); // 二分查找
		
		if (index == -1) { // nums 中不存在 target，直接返回 {-1, -1}
			return new int[] {-1, -1}; // 匿名数组 
		}
		// nums 中存在 targe，则左右滑动指针，来找到符合题意的区间
		int left = index;
		int right = index;
        // 向左滑动，找左边界
		while (left - 1 >= 0 && nums[left - 1] == nums[index]) { // 防止数组越界。逻辑短路，两个条件顺序不能换
			left--;
		}
        // 向左滑动，找右边界
		while (right + 1 < nums.length && nums[right + 1] == nums[index]) { // 防止数组越界。
			right++;
		}
		return new int[] {left, right};
    }
	
	/**
	 * 二分查找
	 * @param nums
	 * @param target
	 */
	public int binarySearch(int[] nums, int target) {
		int left = 0;
		int right = nums.length - 1; // 不变量：左闭右闭区间
		
		while (left <= right) { // 不变量：左闭右闭区间
			int mid = left + (right - left) / 2;
			if (nums[mid] == target) {
				return mid;
			} else if (nums[mid] < target) {
				left = mid + 1;
			} else {
				right = mid - 1; // 不变量：左闭右闭区间
			}
		}
		return -1; // 不存在
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
编辑 (opens new window)
上次更新: 2023/09/13, 12:29:52
IO设备管理
栈与队列

← 栈与队列→

最近更新
01
51单片机及补充知识
09-13
02
独立按键
09-13
03
LCD1602液晶显示器
09-13
更多文章>
Theme by Vdoing | Copyright © 2019-2023 Evan Xu | MIT License