二叉树(中)

# 二叉树(中)

# 六、翻转二叉树

226. 翻转二叉树 - 力扣（LeetCode） (opens new window)

# 1、题目

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。
示例 1：

输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]
1
2
3
4
示例 2：
输入：root = [2,1,3]
输出：[2,3,1]
1
2
3
示例 3：

输入：root = []
输出：[]
1
2
3
4
提示：

树中节点数目范围在 [0, 100] 内

-100 <= Node.val <= 100

# 2、思路

这道题的思路很简单,就是遍历每一个节点,然后对他们的左右指针进行交换,所以写法有很多,比较需要注意的是递归的中序写法
上面加粗这句很重要,是解题的核心
- 这也是为什么所有所有遍历方式基本都可以的原因,因为我们这道题的核心就是要遍历每个节点而已
题目给出的节点定义

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */

1
2
3
4
5
6
7
8
9

# 3、自己胡乱写的递归😫

//写的时候看到函数有返回值,就想着得有个变量去接收函数调用时的返回值,然后就写的奇奇怪怪的,虽然好像是后序遍历的感觉,但总觉得奇奇怪怪的😰😰😰
struct TreeNode* invertTree(struct TreeNode* root){
    if(root==NULL){
        return NULL ;
    }
    struct TreeNode * l_node =  invertTree(root->left);
    struct TreeNode * r_node =  invertTree(root->right);
    root -> left = r_node;
    root -> right = l_node;
    
    return root;
}

1
2
3
4
5
6
7
8
9
10
11
12
13

# 4、深度遍历递归

//递归写法的深度遍历，前后遍历都可以，但是中序遍历不行，如果一定要把交换操作放在中间处理的话，那么两次调用递归函数传入的指针必须都为左或右指针，因为中间处理过后，指针被翻转了,那么就变成了 左中左,或者右中右的遍历,就不符合中序遍历定义了
//以下为前序遍历
struct TreeNode* invertTree(struct TreeNode* root){
    if(root == NULL){
        return root;
    }
    struct TreeNode* node = root->left;  //中
    root ->left = root ->right;
    root->right = node;
    invertTree(root ->left); //左
    invertTree(root ->right); //右
    return root;
}

1
2
3
4
5
6
7
8
9
10
11
12
13

# 5、统一写法的深度遍历

//统一写法深度遍历（我称之为空指针标志法），前中后序都可以
struct TreeNode* invertTree(struct TreeNode* root){
    if(root == NULL){
        return root;
    }
    struct TreeNode * stack[200];
    int top=0;
    stack[top++] =root;

    while(top>0){
        //注意获取栈顶元素要栈顶指针减一
        struct TreeNode* node= stack[top-1];
        if(node != NULL){
            top--;  //出栈
            if(node -> right) stack[top++] = node ->right; //  右
            stack[top++]= node;// 中
            stack[top++]= NULL;
            if(node -> left) stack[top++] = node ->left;  // 左

            //右中左出栈就为 左中右即中序遍历
        }
        else {
            top--; //遇到NULL就弹出，并进行处理
            node = stack[--top];
            struct TreeNode * temp = node->left;
            node->left = node->right;
            node->right = temp;
        }
    }
    return root;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

# 6、层序遍历

struct TreeNode* invertTree(struct TreeNode* root){
    if(root==NULL){
        return NULL ;
    }
    struct TreeNode* queue[100];
    int front=0,rear=0;
    queue[rear++] =root;

    while(front != rear){
        int size = rear - front;
        for(int i=0;i<size;i++){
            struct TreeNode * node = queue[front++];
            //交换左右指针
            struct TreeNode * temp = node ->left;
            node ->left = node-> right;
            node ->right = temp;

            //下面哪个先进没区别，因为我们主要是要遍历每个结点然后交他们的左右指针而已
            if(node->right) queue[rear++] = node->right;
            if(node->left) queue[rear++] = node->left;
            
        }
    }
    return root;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

如果有不理解,看代码随想录 (programmercarl.com) (opens new window)

# 七、对称二叉树

101. 对称二叉树 - 力扣（LeetCode） (opens new window)

# 1、题目

给你一个二叉树的根节点 root ，检查它是否轴对称。
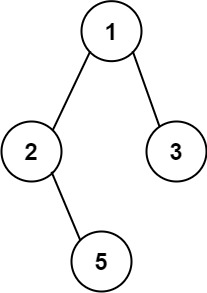
示例 1：
输入：root = [1,2,2,3,4,4,3]
输出：true
1
2
3
示例 2：
输入：root = [1,2,2,null,3,null,3]
输出：false
1
2
3
提示：

树中节点数目在范围 [1, 1000] 内

-100 <= Node.val <= 100

# 2、递归思路

# 2.1 确定递归函数的参数和返回值

因为我们要比较的是根节点的两个子树是否是相互翻转的，进而判断这个树是不是对称树，所以要比较的是两个树，参数自然也是左子树节点和右子树节点。
返回值自然是bool类型。
代码如下：

bool compare(TreeNode* left, TreeNode* right)

# 2.2 确定终止条件

要比较两个节点数值相不相同，首先要把两个节点为空的情况弄清楚！否则后面比较数值的时候就会操作空指针了。
节点为空的情况有：（注意我们比较的其实不是左孩子和右孩子，所以如下我称之为左节点右节点）
- 左节点为空，右节点不为空，不对称，return false
- 左不为空，右为空，不对称 return false
- 左右都为空，对称，返回true
此时已经排除掉了节点为空的情况，那么剩下的就是左右节点不为空：
- 左右都不为空，比较节点数值，不相同就return false
此时左右节点不为空，且数值也不相同的情况我们也处理了。
代码如下：

if (left == NULL && right != NULL) return false;
else if (left != NULL && right == NULL) return false;
else if (left == NULL && right == NULL) return true;
else if (left->val != right->val) return false; // 注意这里我没有使用else

1
2
3
4

注意上面最后一种情况，我没有使用else，而是else if，因为我们把以上情况都排除之后，剩下的就是左右节点都不为空，且数值相同的情况。

# 2.3 确定单层递归的逻辑

此时才进入单层递归的逻辑，单层递归的逻辑就是处理左右节点都不为空，且数值相同的情况。
- 比较二叉树外侧是否对称：传入的是左节点的左孩子，右节点的右孩子。
- 比较内测是否对称，传入左节点的右孩子，右节点的左孩子。
- 如果左右都对称就返回true ，有一侧不对称就返回false 。
代码如下：

bool outside = compare(left->left, right->right);   // 左子树：左、 右子树：右
bool inside = compare(left->right, right->left);    // 左子树：右、 右子树：左
bool isSame = outside && inside;                    // 左子树：中、 右子树：中（逻辑处理）
return isSame;

1
2
3
4

# 3、递归代码

//递归写法
bool compare(struct TreeNode* left,struct TreeNode* right){
    //先排除空节点的情况
    if (left == NULL && right!=NULL) return false;
    else if (left!=NULL && right ==NULL) return false;
    else if (left == NULL && right == NULL) return true;
    //排除无空节点，但数组不同情况
    else if (left->val != right ->val) return false;

    //剩下就是左右节点不为空，且数组相同
    //此时才做递归，做下一层判断
    bool outside = compare(left->left,right ->right); //左子树：左、右子树：右
    bool inside = compare(left->right,right ->left);  //左子树：右、右子树：左
    bool isSame = outside && inside;        //左子树：中、右子树：中（逻辑处理）
    return isSame;
}

bool isSymmetric(struct TreeNode* root){
   if(root == NULL) return true;
   return compare(root->left,root->right);
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

# 4、迭代思路

因为这道题的迭代使用队列或者栈都是一个思路,写发也区别不大,所以就用队列来讲解思路
通过队列来判断根节点的左子树和右子树的内侧和外侧是否相等，如动画所示：

101.对称二叉树

简单来说: 就是把要判断的一对一起放进队列/栈里,判断处理时也一起出队/栈
- 注意处理时, 判断节点都为空就 continue跳过;
- 遇到不对称情况就直接返回 false;
- 除此之外 , 正常两个节点的子节点进队/栈,同时放回 true

# 5、迭代代码

//队列写法，要比较的一对一对进队，出队处理
bool isSymmetric(struct TreeNode* root){
    if(root == NULL) return true;
    struct TreeNode* queue[1000];
    int front=0,rear=0;
    queue[rear++] = root->left;
    queue[rear++] = root->right;

    while(front != rear){
        struct TreeNode* l_node = queue[front++];
        struct TreeNode* r_node = queue[front++];
        //左右节点都都为空 
        if(!l_node && !r_node) continue;
        
        // 左右节点有一个为空，或者都不为空但数组不同
        if(!l_node || !r_node || (l_node ->val != r_node ->val)){
            return false;
        }

        queue[rear++] = l_node->left;
        queue[rear++] = r_node->right;
        queue[rear++] = l_node->right;
        queue[rear++] = r_node->left;

    }
    return true;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

//栈写法，要比较的一对一对进栈，出队处理 （和队列没有太大区别）
bool isSymmetric(struct TreeNode* root){
    if(root == NULL) return true;
    struct TreeNode* stack[1000];
    int top=0;
    stack[top++] = root->left;
    stack[top++] = root->right;

    while(top>0){
        struct TreeNode* l_node =  stack[--top];
        struct TreeNode* r_node =  stack[--top];
        //左右节点都都为空 
        if(!l_node && !r_node) continue;
        
        // 左右节点有一个为空，或者都不为空但数组不同
        if(!l_node || !r_node || (l_node ->val != r_node ->val)){
            return false;
        }

         stack[top++] = l_node->left;
         stack[top++] = r_node->right;
         stack[top++] = l_node->right;
         stack[top++] = r_node->left;

    }
    return true;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

# 6、相似题

# 6.1 100.相同的树

100. 相同的树 - 力扣（LeetCode） (opens new window)
思路:与对称二叉树相似,但是不是按里侧外侧来判断,而是左对左,右对右的判断

# 6.2 572.另一个树的子树😣

572. 另一棵树的子树 - 力扣（LeetCode） (opens new window)

思路：这题比较难，用了双重递归，先递归找到与子树根结点数组相同的结点，然后再递归判断子树是否完全相同

# 八、N叉树的最大深度

559. N 叉树的最大深度 - 力扣（LeetCode） (opens new window)

代码随想录 (programmercarl.com) (opens new window)

上面链接虽然是二叉树的最大深度，但是也有N叉树的

# 1、题目

给定一个 N 叉树，找到其最大深度。

最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。

N 叉树输入按层序遍历序列化表示，每组子节点由空值分隔（请参见示例）。
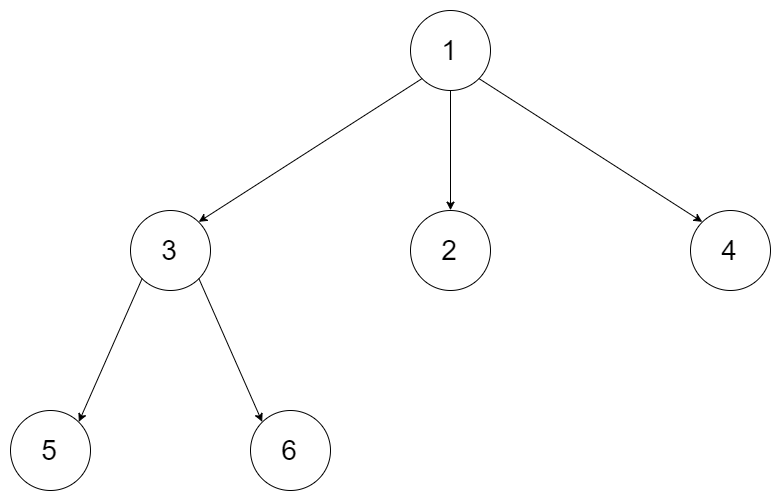
示例 1：

输入：root = [1,null,3,2,4,null,5,6]
输出：3
1
2
3
4
提示：

树的深度不会超过 1000 。

树的节点数目位于 [0, 104] 之间。
/**
 * Definition for a Node.
 * struct Node {
 *     int val;
 *     int numChildren;
 *     struct Node** children;
 * };
 */
1
2
3
4
5
6
7
8

# 2、递归

# 2.1 思路与代码

递归到每个子结点的最深层，然后判断深度，再加1 ，就得到了N叉树的最大深度

//递归
int maxDepth(struct Node* root) {
    //终止条件
    if( root == NULL) return 0;
    //递归处理
    int depth = 0;
    for(int i=0;i<root->numChildren;i++){
        int newdepth = maxDepth(root->children[i]);
        depth = depth > newdepth ? depth : newdepth;
    }
    return depth+1;
}

1
2
3
4
5
6
7
8
9
10
11
12

# 3、迭代

# 3.1 思路与代码

一层一层入队，每进一层，深度加一

//队列写法
int maxDepth(struct Node* root) {
    if(root == NULL) return 0;
    struct Node* queue[10000];
    int front=0,rear=0;
    queue[rear++] = root;
    int depth=0;

    while(front != rear)
    {
        int size = rear - front;
        for(int i=0;i<size;i++)
        {
            struct Node * node = queue[front++];
            for(int k=0;k < node-> numChildren; k++)
            {
                queue[rear++] = node->children[k];
            }
        }
        depth++;
    }
    return depth;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

# 九、完全二叉树

222. 完全二叉树的节点个数 - 力扣（LeetCode） (opens new window)

代码随想录 (programmercarl.com) (opens new window)

# 1、题目

给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。
示例 1：
输入：root = [1,2,3,4,5,6]
输出：6

示例 2：
输入：root = []
输出：0

示例 3：
输入：root = [1]
输出：1
1
2
3
4
5
6
7
8
9
10
11
提示：

树中节点的数目范围是[0, 5 * 104]

0 <= Node.val <= 5 * 104

题目数据保证输入的树是 完全二叉树

# 2、递归思路及代码

后序递归遍历，先求它的左子树的节点数量，再求右子树的节点数量，最后取总和再加一（加1是因为算上当前中间节点）就是目前节点为根节点的节点数量

int countNodes(struct TreeNode* root){
    //递归终止条件
    if(root == NULL){
        return 0;
    }

    int leftnum = countNodes(root->left);   //左
    int rightnum = countNodes(root -> right);  //右
    return 1+ leftnum +rightnum;  //中

}

1
2
3
4
5
6
7
8
9
10
11

# 3、迭代法思路及代码

遍历每个节点，记录数值加一

//栈，迭代
int countNodes(struct TreeNode* root){
    if(root == NULL) return 0;
    struct TreeNode* stack[25000];
    int top=0;
    stack[top++] = root;
    int count=0;

    while(top > 0){
        struct TreeNode* node = stack[--top];
        count++;
        if(node ->left) stack[top++] = node ->left;
        if(node ->right) stack[top++] = node ->right;
    }
    return count;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

//迭代，队列
int countNodes(struct TreeNode* root){
    int count=0;
    if(root == NULL) return count;
    struct TreeNode * queue[50000];
    int front=0,rear=0;
    queue[rear++] = root;
    count++;

    while(front != rear){
        int size= rear -front;
        for(int i=0;i<size;i++){
            struct TreeNode * node = queue[front++];
            if(node -> left) {
                queue[rear++] = node -> left;
                count++;
            }
            if(node -> right) {
                queue[rear++] = node -> right;
                count++;
            }
        }
    }
    return count;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

# 4、完全二叉树性质解法

这道题给我们的就是完全二叉树，所以我们可以利用完全二叉树的性质来解
完全二叉树只有两种情况，情况一：就是满二叉树，情况二：最后一层叶子节点没有满。
- 对于情况一，可以直接用 2^树深度 - 1 来计算，注意这里根节点深度为1。
- 对于情况二，分别递归左孩子，和右孩子，递归到某一深度一定会有左孩子或者右孩子为满二叉树，然后依然可以按照情况1来计算。
完全二叉树（一）如图：

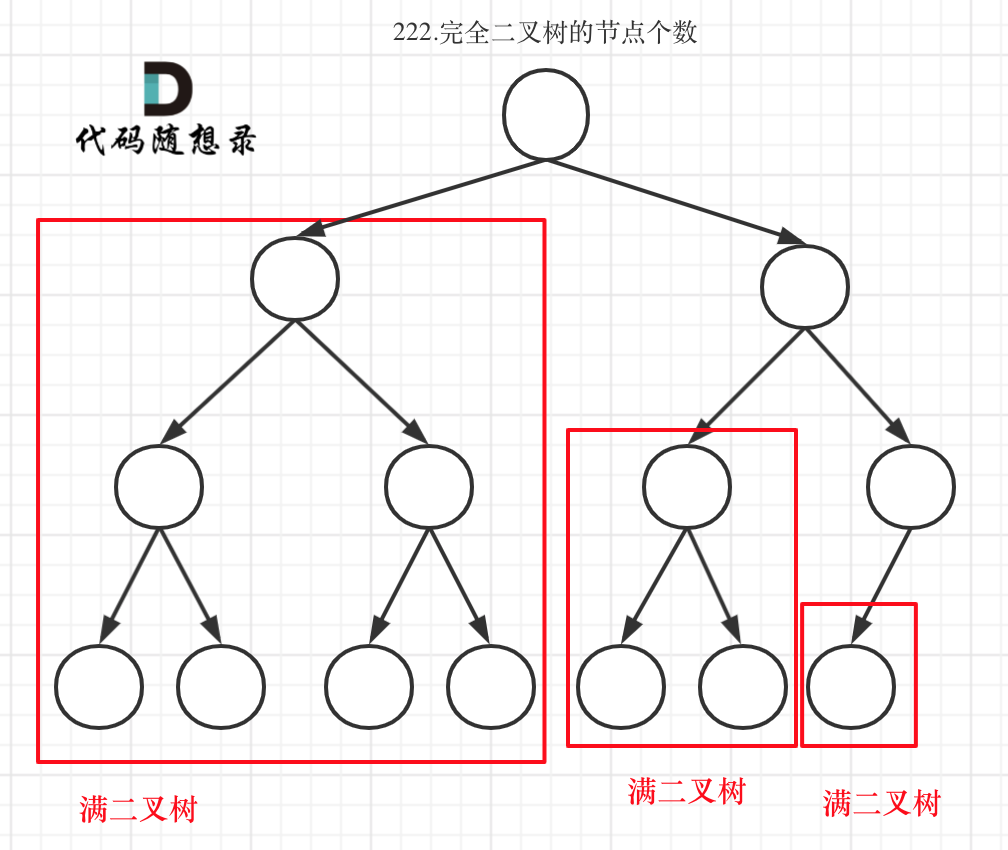
222.完全二叉树的节点个数

完全二叉树（二）如图：
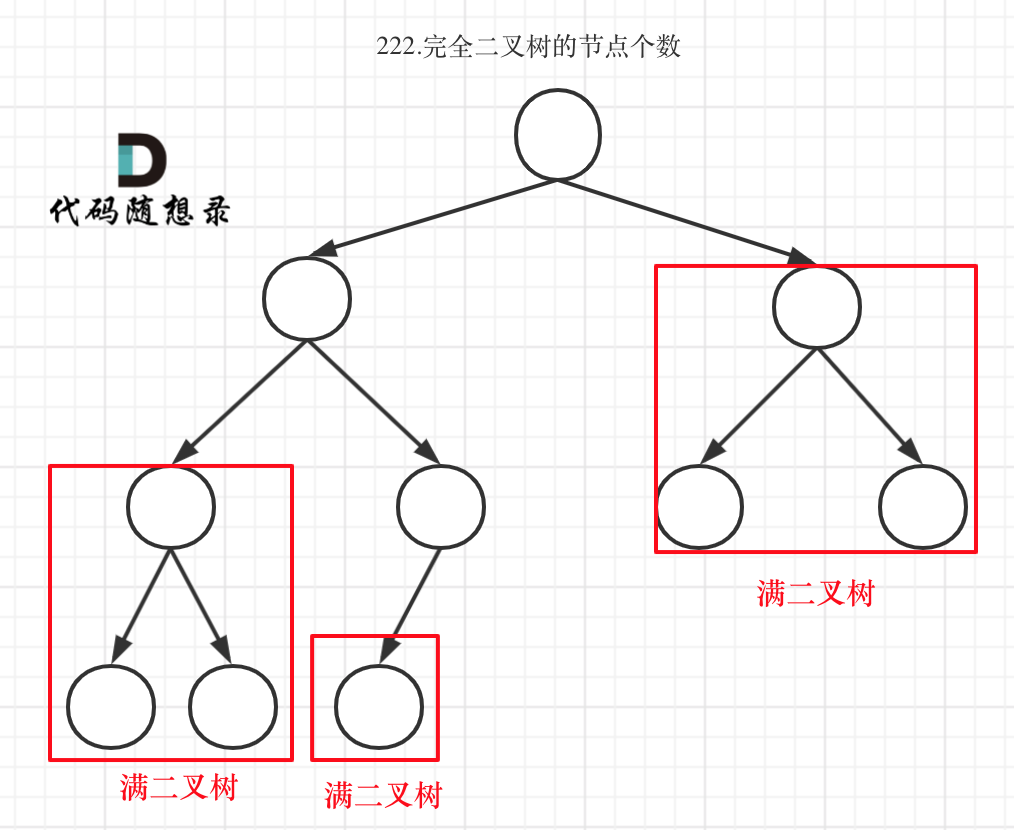
可以看出如果整个树不是满二叉树，就递归其左右孩子，直到遇到满二叉树为止，用公式计算这个子树（满二叉树）的节点数量。
这里关键在于如何去判断一个左子树或者右子树是不是满二叉树呢？
在完全二叉树中，如果递归向左遍历的深度等于递归向右遍历的深度，那说明就是满二叉树。如图：

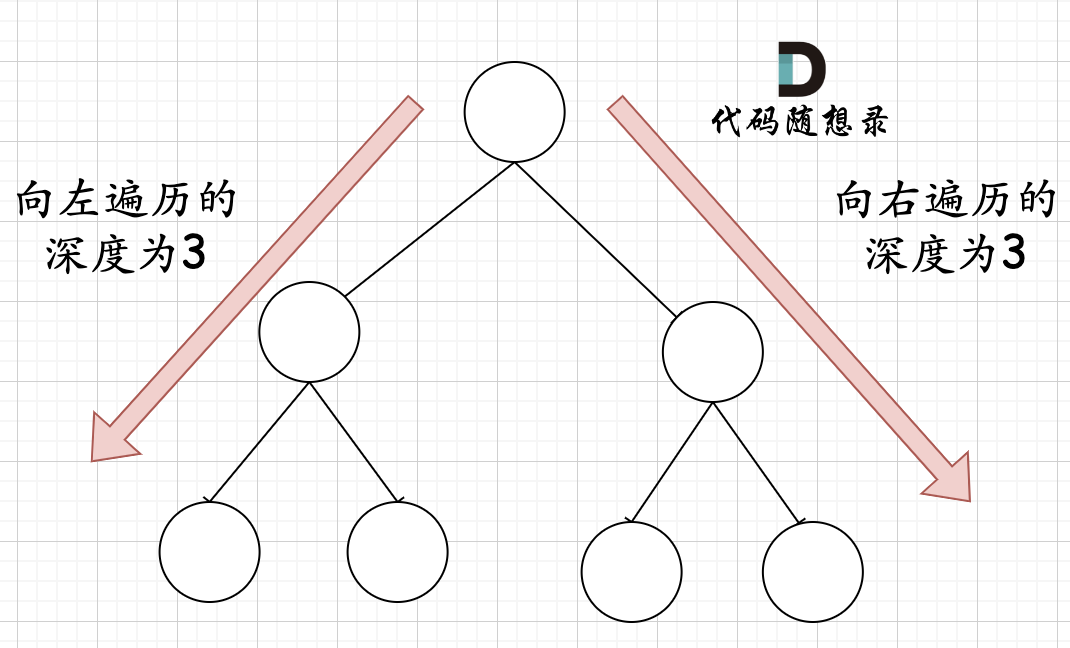
注意：下图虽然递归向左遍历的深度和向右深度相同，但并不是满二叉树，因为它甚至不是完全二叉树，本题给我们的树本身就是完全二叉树，所以我们才可以使用这种判断左右深度的方法来解题

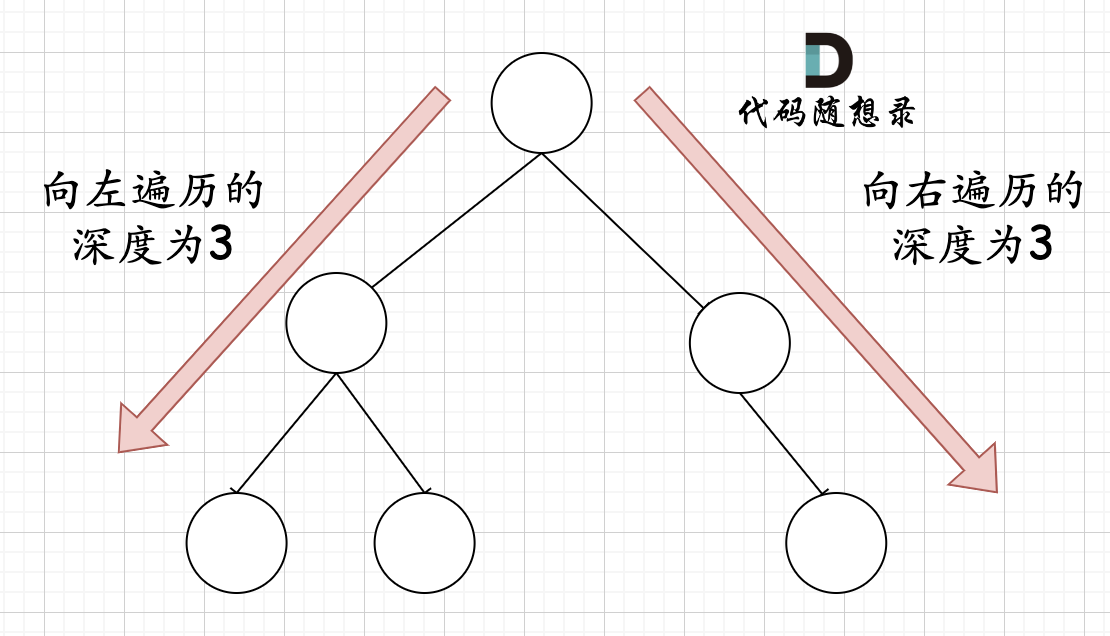
//完全二叉树性质
int countNodes(struct TreeNode* root){
    //递归终止条件
    if(root==NULL)
        return 0;
    int leftDepth = 0;
    int rightDepth = 0;

    struct TreeNode* leftnode =root ->left;
    struct TreeNode* rightnode =root ->right;

    //求出左子树深度
    while(leftnode){
        leftnode = leftnode ->left;
        leftDepth++;
    }
    //求出右子树深度
    while(rightnode){
        rightnode = rightnode ->right;
        rightDepth++;
    }

    //若左右子树深度相同，为满二叉树。结点个数为 2^height-1
    if(rightDepth == leftDepth){
        if(leftDepth == 0)
        //用左移来计算平方
            return (2 << leftDepth) -1;
    }
    //否则返回左右子树的结点个数 +1
    return countNodes(root -> right) + countNodes(root -> left) + 1;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

# 十、平衡二叉树

# 1、题目

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点的左右两个子树的高度差的绝对值不超过 1 。
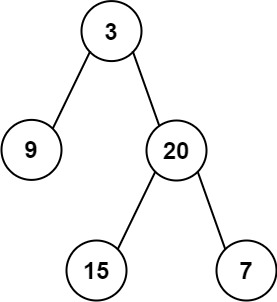
示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：true
1
2
3
4
示例 2：

输入：root = [1,2,2,3,3,null,null,4,4]
输出：false
1
2
3
4
示例 3：
输入：root = []
输出：true
1
2
3
提示：

树中的节点数在范围 [0, 5000] 内 -104 <= Node.val <= 104

# 2、递归思路

注意一个概念：

二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数。

求深度一般用的（前序遍历）
求二叉树的最大深度 (opens new window) 这题用后序遍历是因为，我们这求得就相当于是求根节点的高度

class Solution {
public:
    int result;
    void getDepth(TreeNode* node, int depth) {
        result = depth > result ? depth : result; // 中

        if (node->left == NULL && node->right == NULL) return ;

        if (node->left) { // 左
            depth++;    // 深度+1
            getDepth(node->left, depth);
            depth--;    // 回溯，深度-1
        }
        if (node->right) { // 右
            depth++;    // 深度+1
            getDepth(node->right, depth);
            depth--;    // 回溯，深度-1
        }
        return ;
    }
    int maxDepth(TreeNode* root) {
        result = 0;
        if (root == NULL) return result;
        getDepth(root, 1);
        return result;
    }
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数。
- 求高度一般用（后序遍历）

经过上面分析，我们判断出这道题也需要用后序遍历
- 主要的思路就是，递归遍历每个节点，获取其左右子节点的高度，然后进行比较，要是不满足平衡二叉树的规则，那么就一直返回 -1，否则返回根节点的高度

# 3、递归代码

int height(struct TreeNode * root){
    //递归终止条件
    if(root ==NULL) return 0;

    //递归处理
    int left_h = height(root ->left);
    int right_h = height(root ->right);
    //遇到一次不满足后一直返回 -1
    if(fabs(left_h - right_h) >1 || left_h == -1 ||right_h ==-1){
        return -1;
    }
    //计算高度
    else {
        int height = left_h > right_h ? left_h : right_h;
        return height +1;
    }
}

bool isBalanced(struct TreeNode* root){
    return height(root) > -1;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

# 4、迭代思路

在104.二叉树的最大深度 (opens new window) (opens new window)中我们可以使用层序遍历来求深度，但是就不能直接用层序遍历来求高度了，这就体现出求高度和求深度的不同。
本题的迭代方式可以先定义一个函数，专门用来求高度。
这个函数通过栈模拟的后序遍历找每一个节点的高度（其实是通过求传入节点为根节点的最大深度来求的高度）
然后再用栈来模拟后序遍历，遍历每一个节点的时候，再去判断左右孩子的高度是否符合，代码如下：

//计算结点深度
int getDepth(struct TreeNode* node) {
    //开辟栈空间
    struct TreeNode** stack = (struct TreeNode**)malloc(sizeof(struct TreeNode*) * 10000);
    int stackTop = 0;
    //若传入结点存在，将其入栈。若不存在，函数直接返回0
    if(node)
        stack[stackTop++] = node;
    int result = 0;
    int depth = 0;

    //当栈中有元素时，进行迭代遍历
    while(stackTop) {
        //取出栈顶元素
        struct TreeNode* tempNode = stack[--stackTop];
        //若栈顶元素非NULL，则将深度+1
        if(tempNode) {
            depth++;
            //将栈顶元素再次入栈，添加NULL表示此结点已被遍历
            stack[stackTop++] = tempNode;
            stack[stackTop++] = NULL;
            //若栈顶元素有左右孩子，则将孩子结点入栈
            if(tempNode->left)
                stack[stackTop++] = tempNode->left;
            if(tempNode->right)
                stack[stackTop++] = tempNode->right;
            //更新结果
            result = result > depth ? result : depth;
        }
        else {
            //若为NULL，则代表当前结点已被遍历，深度-1
            tempNode = stack[--stackTop];
            depth--;
        }
    }

    return result;
}

bool isBalanced(struct TreeNode* root){
    //开辟栈空间
    struct TreeNode** stack = (struct TreeNode**)malloc(sizeof(struct TreeNode*) * 10000);
    int stackTop = 0;

    //若根节点不存在，返回True
    if(!root)
        return 1;

    //将根节点入栈
    stack[stackTop++] = root;
    //当栈中有元素时，进行遍历
    while(stackTop) {
        //将栈顶元素出栈
        struct TreeNode* node = stack[--stackTop];
        //计算左右子树的深度
        int diff = getDepth(node->right) - getDepth(node->left);
        //若深度的绝对值大于1，返回False
        if(diff > 1 || diff < -1)
            return 0;
        //如果栈顶结点有左右结点，将左右结点入栈
        if(node->left)
            stack[stackTop++] = node->left;
        if(node->right)
            stack[stackTop++] = node->right;
    }
    //若二叉树遍历结束后没有返回False，则返回True
    return 1;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68

# 十一、二叉树的所有路径

257. 二叉树的所有路径 - 力扣（LeetCode） (opens new window)

# 1、题目

给你一个二叉树的根节点 root ，按任意顺序，返回所有从根节点到叶子节点的路径。

叶子节点是指没有子节点的节点。
示例 1：
输入：root = [1,2,3,null,5]
输出：["1->2->5","1->3"]
1
2
3
示例 2：
输入：root = [1]
输出：["1"]
1
2
3
提示：

树中节点的数目在范围 [1, 100] 内 -100 <= Node.val <= 100
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
1
2
3
4
5
6
7
8
9
10
11
12

# 2、递归写法

1、创建一个数组来保存每层遍历到的结点的值
2、递归函数
- 当递归到叶子节点时，进行字符串处理
- 如果不是叶子节点，就将当前节点的值保存进数组里，然后继续递归

void construct_paths(struct TreeNode*root,char **paths,int* returnSize,int*sta,int top){
    if(root != NULL){
        if(root->left ==NULL && root ->right == NULL){ //当前节点是叶子节点
            char* tmp =(char*)malloc(1001);
            int len =0;
            for(int i=0;i<top;i++){
                //sprintf 会返回写入的字符数
                //tem是char指针，每次 +1，都是tmp中存储的地址值就 +1
                len+=sprintf(tmp + len, "%d->",sta[i]);
            } 
              //最后一个需要单独处理
            sprintf(tmp+len,"%d",root ->val);
            paths[(*returnSize)++] =tmp;
        }
        else{
            sta[top++]=root->val; //当前节点不是叶子节点，继续递归遍历
            construct_paths(root->left,paths,returnSize,sta,top);
            construct_paths(root->right,paths,returnSize,sta,top);
        }
    }
}

char ** binaryTreePaths(struct TreeNode* root, int* returnSize){
    char ** paths = (char**)malloc(sizeof(char*) * 1001);
    * returnSize =0;
    //用来临时存储结点
    int sta[1001];
    //下面传入 returnSize 是传入地址，*returnSize是解引用的意思
    construct_paths(root,paths,returnSize,sta,0);
    return paths;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

# 3、迭代写法

char** binaryTreePaths(struct TreeNode* root, int* returnSize) {
    char** paths = (char**)malloc(sizeof(char*) * 1001);
    *returnSize = 0;
    if (root == NULL) {
        return paths;
    }

    struct TreeNode** node_queue = (struct TreeNode**)malloc(sizeof(struct TreeNode*) * 1001);
    char** path_queue = (char**)malloc(sizeof(char*) * 1001);

    int left = 0, right = 0;

    char* tmp = malloc(sizeof(char) * 1001);
    sprintf(tmp, "%d", root->val);
    node_queue[right] = root;
    path_queue[right++] = tmp;

    while (left < right) {
        struct TreeNode* node = node_queue[left];
        char* path = path_queue[left++];

        if (node->left == NULL && node->right == NULL) {
            paths[(*returnSize)++] = path;
        } else {
            int n = strlen(path);
            if (node->left != NULL) {
                char* tmp = malloc(sizeof(char) * 1001);
                for (int i = 0; i < n; i++) {
                    tmp[i] = path[i];
                }
                sprintf(tmp + n, "->%d", node->left->val);
                node_queue[right] = node->left;
                path_queue[right++] = tmp;
            }

            if (node->right != NULL) {
                char* tmp = malloc(sizeof(char) * 1001);
                for (int i = 0; i < n; i++) {
                    tmp[i] = path[i];
                }
                sprintf(tmp + n, "->%d", node->right->val);
                node_queue[right] = node->right;
                path_queue[right++] = tmp;
            }
        }
    }
    return paths;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

# 十二、左叶子之和

404. 左叶子之和 - 力扣（LeetCode） (opens new window)

代码随想录 (programmercarl.com) (opens new window)

# 1、题目

给定二叉树的根节点 root ，返回所有左叶子之和。
示例 1：
输入: root = [3,9,20,null,null,15,7] 
输出: 24 
解释: 在这个二叉树中，有两个左叶子，分别是 9 和 15，所以返回 24
1
2
3
4
示例 2:
输入: root = [1]
输出: 0
1
2
3
提示:

节点数在 [1, 1000] 范围内

-1000 <= Node.val <= 1000

# 2、什么是左叶子

首先要注意是判断左叶子，不是二叉树左侧节点，所以不要上来想着层序遍历。
- 因为题目中其实没有说清楚左叶子究竟是什么节点，那么我来给出左叶子的明确定义：节点A的左孩子不为空，且左孩子的左右孩子都为空（说明是叶子节点），那么A节点的左孩子为左叶子节点
大家思考一下如下图中二叉树，左叶子之和究竟是多少？

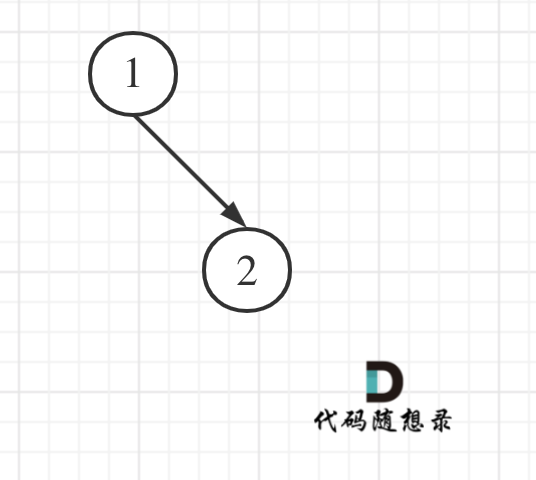
404.左叶子之和

其实是0，因为这棵树根本没有左叶子！
但看这个图的左叶子之和是多少？

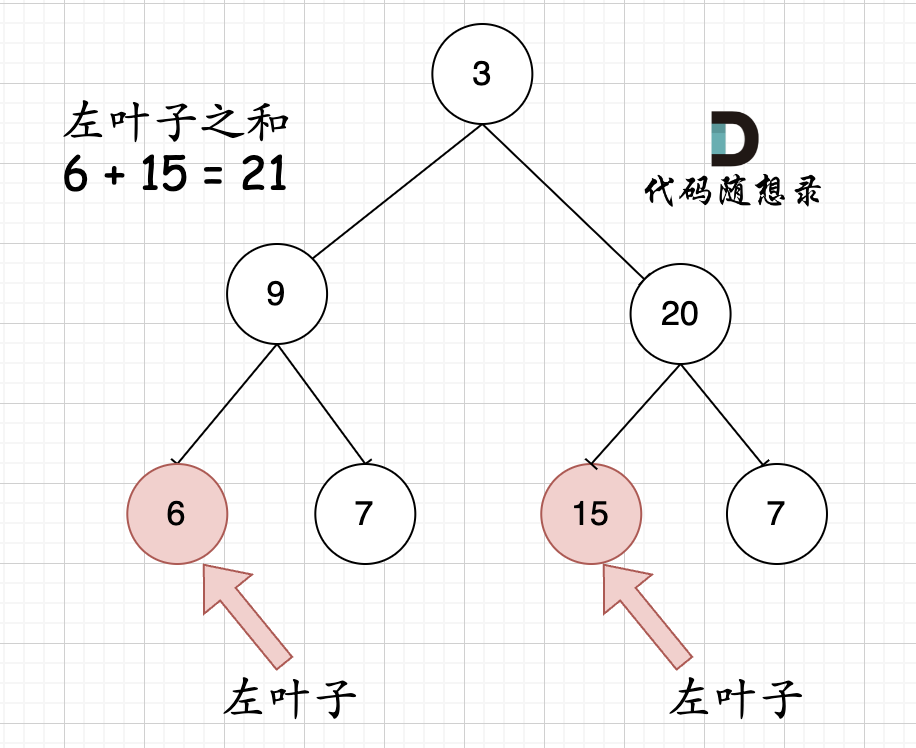
所以判断当前节点是不是左叶子是无法判断的，必须要通过节点的父节点来判断其左孩子是不是左叶子。
如果该节点的左节点不为空，该节点的左节点的左节点为空，该节点的左节点的右节点为空，则找到了一个左叶子，判断代码如下：

if (node->left != NULL && node->left->left == NULL && node->left->right == NULL) {
    左叶子节点处理逻辑
}

1
2
3

# 3、递归写法

递归的遍历顺序为后序遍历（左右中），是因为要通过递归函数的返回值来累加求取左叶子数值之和。
递归三部曲：
1. # 确定递归函数的参数和返回值
判断一个树的左叶子节点之和，那么一定要传入树的根节点，递归函数的返回值为数值之和，所以为int
使用题目中给出的函数就可以了。
1. # 确定终止条件
如果遍历到空节点，那么左叶子值一定是0

if (root == NULL) return 0;

注意，只有当前遍历的节点是父节点，才能判断其子节点是不是左叶子。所以如果当前遍历的节点是叶子节点，那其左叶子也必定是0，那么终止条件为：

if (root == NULL) return 0;
if (root->left == NULL && root->right== NULL) return 0; //其实这个也可以不写，如果不写不影响结果，但就会让递归多进行了一层。

1
2

# 3. 确定单层递归的逻辑
当遇到左叶子节点的时候，记录数值，然后通过递归求取左子树左叶子之和，和右子树左叶子之和，相加便是整个树的左叶子之和。
代码如下：

int leftValue = sumOfLeftLeaves(root->left);    // 左
if (root->left && !root->left->left && !root->left->right) {
    leftValue = root->left->val;
}
int rightValue = sumOfLeftLeaves(root->right);  // 右

int sum = leftValue + rightValue;               // 中
return sum;

1
2
3
4
5
6
7
8

整体递归代码如下：

int sumOfLeftLeaves(struct TreeNode* root){

  //递归终止条件
  if(root == NULL) return 0;
  if(root->left==NULL && root ->right ==NULL) return 0;
  //递归处理
  int leftValue = sumOfLeftLeaves(root->left); //左

  if(root->left != NULL && root->left->left ==NULL && root->left->right ==NULL)
  // 左子树就是一个左叶子的情况
  {
      leftValue= root->left->val;
  }
  int rightValue = sumOfLeftLeaves(root->right); //右
  int sum = leftValue + rightValue; //中

    return sum;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

以上代码精简之后如下：

int sumOfLeftLeaves(struct TreeNode* root){

  //递归终止条件
  if(root == NULL) return 0;
  if(root->left==NULL && root ->right ==NULL) return 0;
  int leftValue=0;
  if(root->left != NULL && root->left->left ==NULL && root->left->right ==NULL)
  {
    leftValue= root->left->val;
  }

    return leftValue + sumOfLeftLeaves(root->left)+sumOfLeftLeaves(root->right);
}

1
2
3
4
5
6
7
8
9
10
11
12
13

精简之后的代码其实看不出来用的是什么遍历方式了，对于算法初学者以上根据第一个版本来学习。

# 4、迭代写法

# 4.1 层序遍历

int sumOfLeftLeaves(struct TreeNode* root){
    int sum =0;
    if(root==NULL) return sum;
    struct TreeNode* queue[2000]; //大小给大点😂，不然测试代码不通过
    int front=0,rear=0;
    queue[rear++] =  root;

    while(front != rear){
        int size = rear- front;
        for(int i=0 ;i<size;i++){
            struct TreeNode* node = queue[front++];
            //判断当前节点是否有左叶子节点
            if(node->left!=NULL&& node->left->left == NULL && node ->left ->right ==NULL){
                sum+= node->left->val;
            }

            if(node->left) queue[rear++] = node ->left;
            if(node->right) queue[rear++] = node ->right;
        }
    }

    return sum;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

# 4.2 深度遍历

//以下是后序遍历的写法，注意我们是看处理节点的顺序里判断是说明遍历顺序的
int sumOfLeftLeaves(struct TreeNode* root){
    int sum =0;
    if(root==NULL) return sum;
    struct TreeNode* stack[2000]; //大小给大点😂，不然测试代码不通过
    int top=0;
    stack[top++] = root;

    while(top>0){
        struct TreeNode* node = stack[top-1];
        if(node != NULL){
            top--;                   
            stack[top++] = node;   //中
            stack[top++]= NULL;
            if(node ->right) stack[top++] = node->right;   //右
             if(node ->left) stack[top++] = node->left;    //左
        }
        else {
            top--; //弹出NULL
            node = stack[--top];//获取要处理的节点
            if(node->left!=NULL&& node->left->left == NULL && node ->left ->right ==NULL){
                sum+= node->left->val;
            }
        }
    }
    return sum;

}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

# 十三、找树左下角的值

513. 找树左下角的值 - 力扣（LeetCode） (opens new window)

# 1、题目

给定一个二叉树的根节点 root，请找出该二叉树的最底层最左边节点的值。

假设二叉树中至少有一个节点。
示例 1:
输入: root = [2,1,3]
输出: 1
1
2
3
示例 2:
输入: [1,2,3,4,null,5,6,null,null,7]
输出: 7
1
2
3
提示:

二叉树的节点个数的范围是 [1,10^4] -2^31 <= Node.val <= 2^31 - 1

# 2、递归思路及写法

递归获取每个节点的深度，判断节点的深度，遇到深度更深的就记录该值，注意我们下面用的前序遍历，（中序遍历应该可以），后序遍历就不可以，因为相同深度的节点我们只记录第一个的值，(即最左)，所以要先遍历左节点

 //递归写法
void traversal(struct TreeNode * root,int depth , int *maxDepth ,int*result){
    if(root->left ==NULL && root -> right ==NULL){   //中
        //遇到深度更深的叶子节点就记录该节点的值
        if(depth > *maxDepth){
            *maxDepth =depth;
            *result =root->val;
        }
    }
    //我们要获取的是最底最左的节点值，所以应该先进左节点
    if(root->left){                                   //左
        depth++;
        traversal(root->left,depth,maxDepth,result);
        depth--;
    }
    if(root->right){                                  //右
        depth++;
        traversal(root->right,depth,maxDepth,result);
        depth--;
    }
    return ;
}

int findBottomLeftValue(struct TreeNode* root){
    int maxDepth = INT_MIN; 
    int result = 0;
    //leetcode c好像不支持用全局变量，执行案例会成功，但是提交代码就会失败
    //所以这里使用指针来操作变量值，所以我们要传入地址
    traversal(root,0,&maxDepth,&result);
    return result;

}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

# 3、层序遍历

这个题的层序遍历比较简单
就正常层序遍历节点，注意我们这里层序遍历先进右节点，再进左节点就可以保证我们想要的值是最后进入队列的

 //层序遍历写法
int findBottomLeftValue(struct TreeNode* root){
    int result = 0;
    if(root==NULL) {
        return result=root->val;
    }

    struct TreeNode* queue[10000];
    int front=0,rear=0;
    queue[rear++] = root;

    while(front != rear){
        int size = rear - front;
        for(int i=0;i<size;i++){
            struct TreeNode* node = queue[front++];  
            //因为我们要的是最深层最左边的节点值，所以我们从右节点先进，就可以保证我们想要的值是最后进入队列的
            if(node->right) queue[rear++] = node ->right;
            if(node->left) queue[rear++] = node ->left;
            
        }
        if(front == rear) {
            result = queue[front-1] ->val;
        }
    }
    return result;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

# 十四、路径总和

112. 路径总和 - 力扣（LeetCode） (opens new window)

代码随想录 (programmercarl.com) (opens new window)

# 1、题目

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

叶子节点 是指没有子节点的节点。
示例 1：
输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出：true
解释：等于目标和的根节点到叶节点路径如上图所示。
1
2
3
4
示例2：
输入：root = [1,2,3], targetSum = 5
输出：false
解释：树中存在两条根节点到叶子节点的路径：
(1 --> 2): 和为 3
(1 --> 3): 和为 4
不存在 sum = 5 的根节点到叶子节点的路径。
1
2
3
4
5
6
7
示例 3：
输入：root = [], targetSum = 0
输出：false
解释：由于树是空的，所以不存在根节点到叶子节点的路径。
1
2
3
4

# 2、递归思路及写法

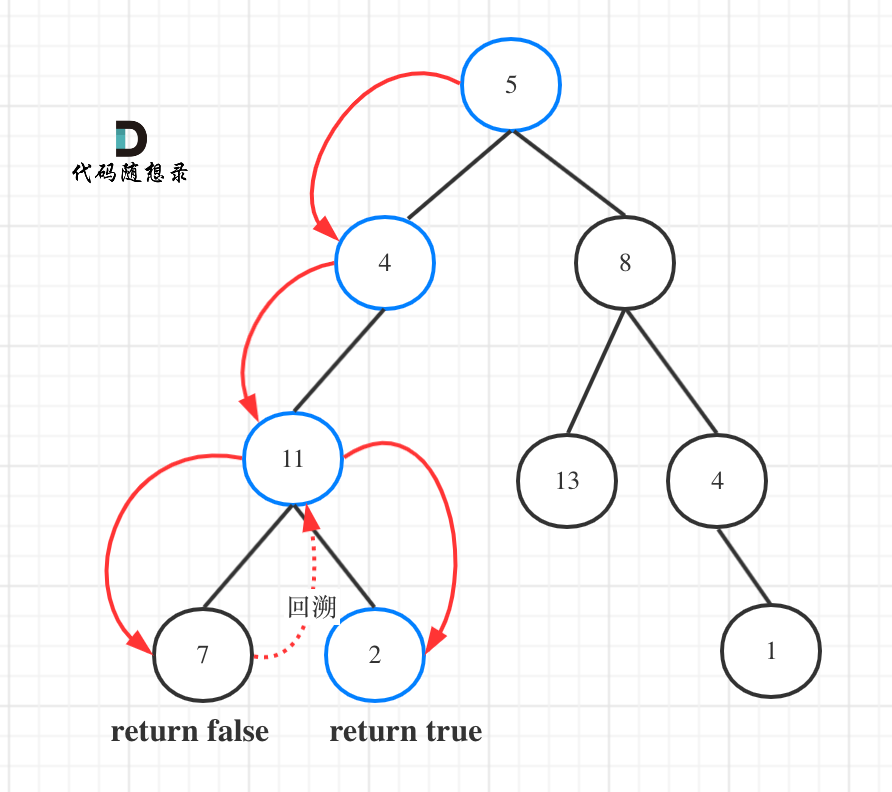
112.路径总和

确定递归函数的参数和返回类型

图中可以看出，遍历的路线，并不要遍历整棵树，所以递归函数需要返回值，可以用bool类型表示。
所以代码如下：

bool traversal(treenode* cur, int count)   // 注意函数的返回类型

确定终止条件

首先计数器如何统计这一条路径的和呢？
不要去累加然后判断是否等于目标和，那么代码比较麻烦，可以用递减，让计数器count初始为目标和，然后每次减去遍历路径节点上的数值。
如果最后count == 0，同时到了叶子节点的话，说明找到了目标和。
如果遍历到了叶子节点，count不为0，就是没找到。
递归终止条件代码如下：

if (!cur->left && !cur->right && count == 0) return true; // 遇到叶子节点，并且计数为0
if (!cur->left && !cur->right) return false; // 遇到叶子节点而没有找到合适的边，直接返回

1
2

确定单层递归的逻辑

因为终止条件是判断叶子节点，所以递归的过程中就不要让空节点进入递归了。
递归函数是有返回值的，如果递归函数返回true，说明找到了合适的路径，应该立刻返回。
代码如下：

if (cur->left) { // 左 （空节点不遍历）
    // 遇到叶子节点返回true，则直接返回true
    if (traversal(cur->left, count - cur->left->val)) return true; // 注意这里有回溯的逻辑
}
if (cur->right) { // 右 （空节点不遍历）
    // 遇到叶子节点返回true，则直接返回true
    if (traversal(cur->right, count - cur->right->val)) return true; // 注意这里有回溯的逻辑
}
return false;

1
2
3
4
5
6
7
8
9

整体代码：

class Solution {
private:
    bool traversal(TreeNode* cur, int count) {
        if (!cur->left && !cur->right && count == 0) return true; // 遇到叶子节点，并且计数为0
        if (!cur->left && !cur->right) return false; // 遇到叶子节点直接返回

        if (cur->left) { // 左
            count -= cur->left->val; // 递归，处理节点;
            if (traversal(cur->left, count)) return true;
            count += cur->left->val; // 回溯，撤销处理结果
        }
        if (cur->right) { // 右
            count -= cur->right->val; // 递归，处理节点;
            if (traversal(cur->right, count)) return true;
            count += cur->right->val; // 回溯，撤销处理结果
        }
        return false;
    }

public:
    bool hasPathSum(TreeNode* root, int sum) {
        if (root == NULL) return false;
        return traversal(root, sum - root->val);
    }
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

精简写法：

bool hasPathSum(struct TreeNode* root, int targetSum){
    // 递归结束条件：若当前节点不存在，返回false
    if(!root)
        return false;
    // 若当前节点为叶子节点，且targetSum-root的值为0。（当前路径上的节点值的和满足条件）返回true
    if(!root->right && !root->left && targetSum == root->val)
        return true;

    // 查看左子树和右子树的所有节点是否满足条件
    return hasPathSum(root->right, targetSum - root->val) || hasPathSum(root->left, targetSum - root->val);
}

1
2
3
4
5
6
7
8
9
10
11

# 3、迭代思路及写法

1. 构建一个结构体 Pair，用来存放节点，和到达对应节点的路径值

// 存储一个节点以及当前的和
struct Pair {
    struct TreeNode* node;
    int sum;
};

1
2
3
4
5

1. 判断，若栈顶元素为叶子节点，且和为targetSum时，返回true

// 若栈顶元素为叶子节点，且和为targetSum时，返回true
   if(!topPair.node->left && !topPair.node->right && topPair.sum == targetSum){
         return true;
    }

1
2
3
4

若当前栈顶节点有左右孩子，计算和并入栈

if(topPair.node->left) {
     struct Pair newPair = {topPair.node->left, topPair.sum + topPair.node->left->val};
     stack[stackTop++] = newPair;
}
if(topPair.node->right) {
     struct Pair newPair = {topPair.node->right, topPair.sum + topPair.node->right->val};
     stack[stackTop++] = newPair;
}

1
2
3
4
5
6
7
8

整体代码：

// 存储一个节点以及当前的和
struct Pair {
    struct TreeNode* node;
    int sum;
};

bool hasPathSum(struct TreeNode* root, int targetSum){
    struct Pair stack[1000];
    int stackTop = 0;

    // 若root存在，则将节点和值封装成一个pair入栈
    if(root) {
        struct Pair newPair = {root, root->val};
        stack[stackTop++] = newPair;
    }

    // 当栈不为空时
    while(stackTop) {
        // 出栈栈顶元素
        struct Pair topPair = stack[--stackTop];
        // 若栈顶元素为叶子节点，且和为targetSum时，返回true
        if(!topPair.node->left && !topPair.node->right && topPair.sum == targetSum)
            return true;

        // 若当前栈顶节点有左右孩子，计算和并入栈
        if(topPair.node->left) {
            struct Pair newPair = {topPair.node->left, topPair.sum + topPair.node->left->val};
            stack[stackTop++] = newPair;
        }
        if(topPair.node->right) {
            struct Pair newPair = {topPair.node->right, topPair.sum + topPair.node->right->val};
            stack[stackTop++] = newPair;
        }
    }
    return false;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

# 4、自己瞎写

自己一开始看这道题时，瞎写的解法

bool recursion(struct TreeNode* root, int targetSum,int curSum){
    if(root == NULL){
        return false;
    }
    curSum += root->val;
    if(root->left==NULL && root->right==NULL && curSum == targetSum){
        return true;
    }
    return recursion(root->left,targetSum,curSum) || recursion(root-> right,targetSum,curSum);
}

bool hasPathSum(struct TreeNode* root, int targetSum){
    if(root ==NULL){
        return 0;
    }
    return recursion(root,targetSum,0);

}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

# 十五、路径总和2

# 1、题目

给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有从根节点到叶子节点路径总和等于给定目标和的路径。

叶子节点是指没有子节点的节点。
示例1：
输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：[[5,4,11,2],[5,8,4,5]]
1
2
3
示例2：
输入：root = [1,2,3], targetSum = 5
输出：[]
1
2
3
示例3：
输入：root = [1,2], targetSum = 0
输出：[]
1
2
3
提示：

树中节点总数在范围 [0, 5000] 内

-1000 <= Node.val <= 1000

-1000 <= targetSum <= 1000

# 2、思路

创建一个栈和结果队列(二维数组)
递归进入直到最后一层，判断sum数组是否是为指定路劲总和，是就将栈中的元素拷贝个结果数组

递归:

传入参数

void traversal(struct TreeNode *root,int targetSum,int * returnSize,int** returnColumnSizes,int**result,int* stack,int top,int sum)

结束条件

//结束条件
if(root ==NULL) return ;

1
2

3.递归处理

sum += root->val;
    stack[top] = root->val;
    if(root->left==NULL && root ->right==NULL && sum == targetSum){
       //申请空间
       result[*returnSize] = (int*)malloc(sizeof(int)*(top+1));
       //拷贝内容
       memcpy(result[*returnSize],stack,sizeof(int)*(top+1));
       (* returnColumnSizes)[*returnSize] = top +1;
       *returnSize = *returnSize +1;
    }

1
2
3
4
5
6
7
8
9
10

# 3、代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */


/**
 * Return an array of arrays of size *returnSize.
 * The sizes of the arrays are returned as *returnColumnSizes array.
 * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
 */
void traversal(struct TreeNode *root,int targetSum,int * returnSize,int** returnColumnSizes,int**result,int* stack,int top,int sum){
    //结束条件
    if(root ==NULL) return ;
    //执行条件 
    sum += root->val;
    stack[top] = root->val;
    if(root->left==NULL && root ->right==NULL && sum == targetSum){
       //申请空间
       result[*returnSize] = (int*)malloc(sizeof(int)*(top+1));
       //拷贝内容
       memcpy(result[*returnSize],stack,sizeof(int)*(top+1));
       (* returnColumnSizes)[*returnSize] = top +1;
       *returnSize = *returnSize +1;
    }
    //遍历左子树
    traversal(root->left,targetSum,returnSize,returnColumnSizes,result,stack,top+1,sum);
    //遍历右子树
    traversal(root->right,targetSum,returnSize,returnColumnSizes,result,stack,top+1,sum);

}


int** pathSum(struct TreeNode* root, int targetSum, int* returnSize, int** returnColumnSizes) {
    int ** result= (int**)malloc(sizeof(int *)*5000);
    *returnColumnSizes =(int *)malloc(sizeof(int)*5000);
    int stack[5000] = {0}; 
    *returnSize =0;
    traversal(root,targetSum,returnSize,returnColumnSizes,result,stack,0,0);
    return result;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

# 十六、最大二叉树

654. 最大二叉树 - 力扣（LeetCode） (opens new window)

# 1、题目

给定一个不重复的整数数组 nums 。最大二叉树可以用下面的算法从 nums 递归地构建:

创建一个根节点，其值为 nums 中的最大值。递归地在最大值左边的子数组前缀上构建左子树。递归地在最大值右边的子数组后缀上构建右子树。返回 nums 构建的最大二叉树。

示例：1
输入：nums = [3,2,1,6,0,5]
输出：[6,3,5,null,2,0,null,null,1]
解释：递归调用如下所示：
- [3,2,1,6,0,5] 中的最大值是 6 ，左边部分是 [3,2,1] ，右边部分是 [0,5] 。
    - [3,2,1] 中的最大值是 3 ，左边部分是 [] ，右边部分是 [2,1] 。
        - 空数组，无子节点。
        - [2,1] 中的最大值是 2 ，左边部分是 [] ，右边部分是 [1] 。
            - 空数组，无子节点。
            - 只有一个元素，所以子节点是一个值为 1 的节点。
    - [0,5] 中的最大值是 5 ，左边部分是 [0] ，右边部分是 [] 。
        - 只有一个元素，所以子节点是一个值为 0 的节点。
        - 空数组，无子节点。

1
2
3
4
5
6
7
8
9
10
11
12
13

示例2：
输入：nums = [3,2,1]
输出：[3,null,2,null,1]

1
2
3

提示：

1 <= nums.length <= 1000
0 <= nums[i] <= 1000
nums 中的所有整数 互不相同

# 2、思路

找到数组最大值下标，切割左右数组

# 3、代码

struct TreeNode* constructMaximumBinaryTree(int* nums, int numsSize){
    //如果数组大小为0，说明数组为空，返回 NULL
    if(numsSize ==0){
        return NULL;
    }
    //数组不为 NULL
    int maxIndex = 0;
    //找到数组中最大的数坐标，做为切割点
    for(int i=1;i<numsSize;i++){
        if(nums[i] > nums[maxIndex]){
            maxIndex =i;
        }
    }

    //开辟结点
    struct TreeNode* node =(struct TreeNode*)malloc(sizeof(struct TreeNode));
    node->val = nums[maxIndex];

    //递归定义左孩子和右孩子
    int rightSize = numsSize - maxIndex -1;
    //切割左右数组
    node->left = constructMaximumBinaryTree(nums,maxIndex);
    node->right = constructMaximumBinaryTree(nums+maxIndex+1,rightSize);

    return node;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

编辑

上次更新: 2023/09/13, 12:29:52

← 二叉树(上) 二叉树(下)→

二叉树(中)

# 二叉树(中)

# 六、翻转二叉树

# 1、题目

# 2、思路

# 3、自己胡乱写的递归😫

# 4、深度遍历递归

# 5、统一写法的深度遍历

# 6、层序遍历

# 七、对称二叉树

# 1、题目

# 2、递归思路

# 2.1 确定递归函数的参数和返回值

# 2.2 确定终止条件

# 2.3 确定单层递归的逻辑

# 3、递归代码

# 4、迭代思路

# 5、迭代代码

# 6、相似题

# 6.1 100.相同的树

# 6.2 572.另一个树的子树😣

# 八、N叉树的最大深度

# 1、题目

# 2、递归

# 2.1 思路与代码

# 3、迭代

# 3.1 思路与代码

# 九、完全二叉树

# 1、题目

# 2、递归思路及代码

# 3、迭代法思路及代码

# 4、完全二叉树性质解法

# 十、平衡二叉树

# 1、题目

# 2、递归思路

# 3、递归代码

# 4、 迭代思路

# 十一、二叉树的所有路径

# 1、题目

# 2、递归写法

# 3、迭代写法

# 十二、左叶子之和

# 1、题目

# 2、什么是左叶子

# 3、递归写法

# 确定递归函数的参数和返回值

# 确定终止条件

# 3. 确定单层递归的逻辑

# 4、迭代写法

# 4.1 层序遍历

# 4.2 深度遍历

# 十三、找树左下角的值

# 1、题目

# 2、递归思路及写法

# 3、层序遍历

# 十四、路径总和

# 1、题目

# 2、递归思路及写法

# 3、迭代思路及写法

# 4、自己瞎写

# 十五、路径总和2

# 1、题目

# 2、思路

# 3、代码

# 十六、最大二叉树

# 1、题目

# 2、思路

# 3、代码

# 4、迭代思路