JackCin's blog
JackCin
2023-09-13
目录

栈与队列

# 栈与队列

代码随想录 (programmercarl.com) (opens new window)

  • 队列（queue）： 先进先出 ，队尾进，队首出
  • 栈（stack）：先进后出 ，一个指针指向末尾

# 一、用栈实现队列

# 1、题目

232. 用栈实现队列 - 力扣（LeetCode） (opens new window)

请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作（push、pop、peek、empty）：

实现 MyQueue 类：

void push(int x) 将元素 x 推到队列的末尾 int pop() 从队列的开头移除并返回元素 int peek() 返回队列开头的元素 boolean empty() 如果队列为空，返回 true ；否则，返回 false

示例 :

输入：
["MyQueue", "push", "push", "peek", "pop", "empty"]
[[], [1], [2], [], [], []]
输出：
[null, null, null, 1, 1, false]

解释：
MyQueue myQueue = new MyQueue();
myQueue.push(1); // queue is: [1]
myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue)
myQueue.peek(); // return 1
myQueue.pop(); // return 1, queue is [2]
myQueue.empty(); // return false
1
2
3
4
5
6
7
8
9
10
11
12
13

提示：

  • 1 <= x <= 9
  • 最多调用 100 次 push、pop、peek 和 empty
  • 假设所有操作都是有效的 （例如，一个空的队列不会调用 pop 或者 peek 操作）

# 2、思路

  • 使用两个栈 ，stackIn（输入栈）和 stackOut (输出栈) ,当我们需要模拟队列出队（先进先出）时，我们先让 stackIn 按先进后出原则，一个一个出stackIn，并进入stackOut（这样原先stackIn的头元素就会变成stackOut的尾元素）， 然后再弹出并保存stackOut里最后一个元素，之后，再让stackOut按先进后出原则，一个一个出stackOut，再进入stackIn就完成了栈模拟出队的功能。

# 3、代码

typedef struct {
    int stackInTop,stackOutTop;
    int stackIn[100],stackOut[100];
} MyQueue;

//创建队列
MyQueue* myQueueCreate() {
    MyQueue* queue = (MyQueue* )malloc(sizeof(MyQueue));
    queue -> stackInTop = 0;
    queue -> stackOutTop =0;
    return queue;
}

//进入队列
void myQueuePush(MyQueue* obj, int x) {
    obj -> stackIn[(obj->stackInTop)++] =x;
}

//离开队列
/*
1.若输出栈为空且输入栈中有元素，将输入栈中的元素复制到第二个栈中
2、将栈顶元素保存
3、当输出栈>0时，将输出栈中的元素复制到输入栈中
*/
int myQueuePop(MyQueue* obj) {
    //优化：复制栈顶指针，减少对内存的访问次数
    //(可以直接使用obj ->satckInTop 这样的指针形式来写，但是这样每次使用都要对内存进行访问)
    int stackInTop =obj ->stackInTop;
    int stackOutTop = obj -> stackOutTop;
    //1、如果输出栈为空
    if(stackOutTop == 0){
        //将输入栈中的元素复制到输出栈里
        while(stackInTop>0){
           obj -> stackOut[stackOutTop++] =obj -> stackIn[--stackInTop];
        }
    }

    //2、保存栈顶元素
    int top = obj->stackOut[--stackOutTop];

    //3、再将输出栈元素倒回输入栈里
    while(stackOutTop >0 ){
        obj ->stackIn[stackInTop++] = obj -> stackOut[--stackOutTop];
    }

    //4、更新栈顶指针
    obj ->stackInTop = stackInTop;
    obj -> stackOutTop = stackOutTop;

    //5、返回队列的第一个元素
    return top;
}


//返回输入栈中的栈底元素
int myQueuePeek(MyQueue* obj) {
    return obj->stackIn[0];
}

//判断队列是否为空
bool myQueueEmpty(MyQueue* obj) {
    return  obj->stackInTop == 0 ;
    //return  obj->stackInTop == 0 && obj->stackOutTop ==0 ;
}

void myQueueFree(MyQueue* obj) {
    obj-> stackInTop = 0;
    obj -> stackOutTop =0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70

# 二、用队列实现栈

# 1、题目

225. 用队列实现栈 - 力扣（LeetCode） (opens new window)

请你仅使用两个队列实现一个后入先出（LIFO）的栈，并支持普通栈的全部四种操作（push、top、pop 和 empty）。

实现 MyStack 类：

void push(int x) 将元素 x 压入栈顶。 int pop() 移除并返回栈顶元素。 int top() 返回栈顶元素。 boolean empty() 如果栈是空的，返回 true ；否则，返回 false 。

示例 :

输入：
["MyStack", "push", "push", "top", "pop", "empty"]
[[], [1], [2], [], [], []]
输出：
[null, null, null, 2, 2, false]

解释：
MyStack myStack = new MyStack();
myStack.push(1);
myStack.push(2);
myStack.top(); // 返回 2
myStack.pop(); // 返回 2
myStack.empty(); // 返回 False
1
2
3
4
5
6
7
8
9
10
11
12
13

提示：

  • 1 <= x <= 9
  • 最多调用100 次 push、pop、top 和 empty
  • 每次调用 pop 和 top 都保证栈不为空

# 2、思路及代码

# 2.1、使用两个队列

  • 使用两个队列 ，queue1 和 queue2,选其中一个作为辅助队列（以下我们使用queue2作为辅助栈），当我们需要模拟出栈（先进后出）时，我们先让queue1按先进先出原则，一个一个出queue1，并进入queue2（直到queue1里只剩下一个元素）， 然后再弹出并保存queue1里的元素，之后，再让queue2按先进先出原则，一个一个出queue2，再进入queue1就完成了队列模拟出栈的功能。

  • 其他实现比较简单，使用queue1就行。。。。。

typedef struct {
    int queue1[100],queue2[100];
    int front1,front2;
    int rear1,rear2;
} MyStack;

//创建栈
MyStack* myStackCreate() {
    MyStack* stack = (MyStack* )malloc(sizeof(MyStack));
    stack -> front1 = 0 ;
    stack -> front2 = 0 ;
    stack -> rear1 = 0 ;
    stack -> rear2 = 0 ;
    return stack;
}


//入栈
void myStackPush(MyStack* obj, int x) {
    obj -> queue1[(obj->rear1)++] = x;
}

//出栈
/*   
1、把队列1里的元素按先进先出原则，放进队列2里，直到队列1只剩一个元素
2、弹出并保存元素
3、队列2元素回到队列1
*/
int myStackPop(MyStack* obj) {
    //优化： 复制指针，减少对内存的访问
    int front1 = obj->front1,front2 = obj -> front2;
    int rear1 = obj -> rear1, rear2 = obj -> rear2;
    //1. 队列1出进入队列2
    while((rear1 - front1) > 1){
        obj->queue2[rear2++] = obj ->queue1[front1++];
    }

    //2. 弹出并保存队列1最后的元素
    int top = obj->queue1[front1++];
    //3. 队列2元素回到队列1
    while(rear2 - front2 > 0 ){
        obj -> queue1[rear1++] = obj -> queue2[front2++];
    }
    //更新队首队尾指针
    obj -> front1 = front1;
    obj -> front2 = front2;
    obj -> rear1 = rear1;
    obj -> rear2 = rear2;
    //返回栈顶指针
    return top;
}

//返回栈顶元素
int myStackTop(MyStack* obj) {
    return obj ->queue1[(obj->rear1)-1];
}
//判断栈是否为空
bool myStackEmpty(MyStack* obj) {
    //队列首尾指针相等为空
    return obj->front1 == obj->rear1;
}

//清空栈
void myStackFree(MyStack* obj) {
    obj -> front1 = 0;
    obj -> front2 = 0;
    obj -> rear1 = 0;
    obj -> rear2 = 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70

# 2.2 使用一个队列

  • 使用一个队列 queue，如果要实现出栈的功能，就需要在出队时将，将元素一个一个从队头出队，再重新进入队尾，直到队首指针指向了原先的队尾元素，再弹出并保存该元素，就完成了出栈的功能。
typedef struct {
    int queue[100];
    int front,rear;
} MyStack;

//创建栈
MyStack* myStackCreate() {
    MyStack* stack = (MyStack* )malloc(sizeof(MyStack));
    stack -> front = 0 ;
    stack -> rear = 0 ;
    return stack;
}


//入栈
void myStackPush(MyStack* obj, int x) {
    obj -> queue[(obj->rear)++] = x;
}

int myStackPop(MyStack* obj) {
    //优化： 复制指针，减少对内存的访问
    int front = obj->front;
    int rear = obj -> rear;
    //1.将队列除最后一个元素都出队并重新进队
    int size = rear - front;
    while(size-- > 1){
        obj->queue[rear++] = obj ->queue[front++];
    }
    //2. 弹出并保存队列1最后的元素
    int top = obj->queue[front++];
    //更新队首队尾指针
    obj -> front = front;
    obj -> rear = rear;
    //返回栈顶指针
    return top;
}

//返回栈顶元素
int myStackTop(MyStack* obj) {
    return obj ->queue[(obj->rear)-1];
}
//判断栈是否为空
bool myStackEmpty(MyStack* obj) {
    //队列首尾指针相等为空
    return obj->front == obj->rear;
}

//清空栈
void myStackFree(MyStack* obj) {
    obj -> front = 0;
    obj -> rear = 0;

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

# 三、有效的括号

# 1、题目

20. 有效的括号 - 力扣（LeetCode） (opens new window)

给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

左括号必须用相同类型的右括号闭合。 左括号必须以正确的顺序闭合。 每个右括号都有一个对应的相同类型的左括号。

示例1：
输入：s = "()"
输出：true

示例 2：
输入：s = "()[]{}"
输出：true

示例 3：
入：s = "(]"
输出：false
1
2
3
4
5
6
7
8
9
10
11

提示：

  • 1 <= s.length <= 104
  • s 仅由括号 '()[]{}' 组成

# 2、思路

  • 这道题只要是要解决3种不匹配的情况：

      1. 字符串里左方向的括号多余了 ，所以不匹配；

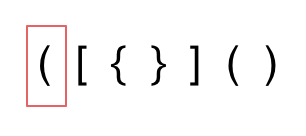
    括号匹配1

      1. 括号没有多余，但是 括号的类型没有匹配上。

    /

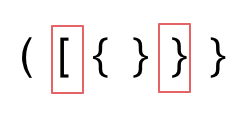
      1. 字符串里右方向的括号多余了，所以不匹配。

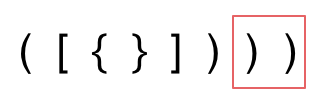
括号匹配3

  • 解决：
    • 第一种情况：已经遍历完了字符串，但是栈不为空，说明有相应的左括号没有右括号来匹配，所以return false
    • 第二种情况：遍历字符串匹配的过程中，发现栈里没有要匹配的字符。所以return false
    • 第三种情况：遍历字符串匹配的过程中，栈已经为空了，没有匹配的字符了，说明右括号没有找到对应的左括号return false

20.有效括号

# 3、代码

bool notMatch(char par,char* stack,int stackTop){
    switch(par){
        case ']':
            return stack[stackTop - 1] != '[';
        case ')':
            return stack[stackTop - 1] != '(';
        case '}':
            return stack[stackTop - 1] != '{';
    }
    return 0;
};

bool isValid(char * s){
    int strLen = strlen(s);
    //开辟栈空间
    char stack[5000]; // s的长度范围为1~10000，如果有对应的就会
    int stackTop =0;

    //遍历字符串
    int i;
    for(i=0;i<strLen;i++)
    {
        char tempChar = s[i];
        //如果当前字符为左字符，则直接进栈
        if(tempChar == '(' || tempChar == '[' || tempChar == '{')
        {
            stack[stackTop++] = tempChar;
        }
        //如果当前元素为右括号，且栈顶元素不匹配或者栈中无元素，则直接返回false
        else if(stackTop == 0 || notMatch(tempChar,stack,stackTop))
        {
            return false;
        }
        //如果匹配后，栈顶元素匹配
        else {
            stackTop--; //栈顶元素出栈
        }
    }
    return stackTop == 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

# 四、删除字符串中的所有相邻重复项

1047. 删除字符串中的所有相邻重复项 - 力扣（LeetCode） (opens new window)

# 1、题目

给出由小写字母组成的字符串 S，重复项删除操作会选择两个相邻且相同的字母，并删除它们。

在 S 上反复执行重复项删除操作，直到无法继续删除。

在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。

示例：

输入："abbaca"
输出："ca"
解释：
例如，在 "abbaca" 中，我们可以删除 "bb" 由于两字母相邻且相同，这是此时唯一可以执行删除操作的重复项。之后我们得到字符串 "aaca"，其中又只有 "aa" 可以执行重复项删除操作，所以最后的字符串为 "ca"。
1
2
3
4
5
6

提示：

1 <= S.length <= 20000 S 仅由小写英文字母组成。

# 2、思路

这道题有使用栈和双指针两种写法：

思路都比较简单，主要是逻辑判断有点小细节，看代码吧😂

# 3、代码

# 3.1 栈写法

char * removeDuplicates(char * s){
    int len = strlen(s);
    char * stack = (char* )malloc(sizeof(char)* len +1);
    int stackTop = 0;

    for(int i=0; i< strlen(s); i++){
        //如果栈不为空，且栈顶元素相同，则栈顶元素弹出
        if( stackTop != 0 && s[i] == stack[stackTop -1]){
            stackTop--;
        }
        //如果为空，或者匹配则直接进栈
        else {
            stack[stackTop++] = s[i];
        }
    }
    //字符串最后必须给 \0
    stack[stackTop] = '\0';
    return stack;

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

# 3.2 双指针

  • 这个是我自己写的双指针，晚上急着写的，感觉可以再修改修改😣
    • 又想了一下，感觉这样写也还行😂
char * removeDuplicates(char * s){
    int fast =0;
    int slow =-1;
    while(fast < strlen(s)){
        if(slow == -1){
            s[++slow] = s[fast];
        }
        else if(slow != -1 && s[slow] != s[fast]){
            s[++slow] = s[fast];
        }
        else {
            slow--;c
        }
        fast++;
    }
    s[slow+1] = '\0';
    return s;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

  • 这个是卡尔老师的

  • char * removeDuplicates(char * s){
    //创建快慢指针
    int fast = 0;
    int slow = 0;
    //求出字符串长度
    int strLength = strlen(s);
    //遍历字符串
    while(fast < strLength) {
        //将当前slow指向字符改为fast指向字符。fast指针+1
        char letter = s[slow] = s[fast++];
        //若慢指针大于0，且慢指针指向元素等于字符串中前一位元素，删除慢指针指向当前元素
        if(slow > 0 && letter == s[slow - 1])
            slow--;
        else
            slow++;
    }c
    //在字符串结束加入字符串结束标志'\0'
    s[slow] = 0;
    return s;
}
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20

# 五、 逆波兰表达式求值

150. 逆波兰表达式求值 - 力扣（LeetCode） (opens new window)

# 1、题目

给你一个字符串数组 tokens ，表示一个根据 逆波兰表示法 表示的算术表达式。

请你计算该表达式。返回一个表示表达式值的整数。

注意：

有效的算符为 '+'、'-'、'*' 和 '/' 。 每个操作数（运算对象）都可以是一个整数或者另一个表达式。 两个整数之间的除法总是 向零截断 。 表达式中不含除零运算。 输入是一个根据逆波兰表示法表示的算术表达式。 答案及所有中间计算结果可以用 32 位 整数表示。

示例 1：

输入：tokens = ["2","1","+","3","*"]
输出：9
解释：该算式转化为常见的中缀算术表达式为：((2 + 1) * 3) = 9
示例 2：

输入：tokens = ["4","13","5","/","+"]
输出：6
解释：该算式转化为常见的中缀算术表达式为：(4 + (13 / 5)) = 6
示例 3：

输入：tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5","+"]
输出：22c
解释：该算式转化为常见的中缀算术表达式为：
  ((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

提示：

1 <= tokens.length <= 104 tokens[i] 是一个算符（"+"、"-"、"*" 或 "/"），或是在范围 [-200, 200] 内的一个整数

逆波兰表达式：

逆波兰表达式是一种后缀表达式，所谓后缀就是指算符写在后面。

平常使用的算式则是一种中缀表达式，如 ( 1 + 2 ) * ( 3 + 4 ) 。 该算式的逆波兰表达式写法为 ( ( 1 2 + ) ( 3 4 + ) * ) 。 逆波兰表达式主要有以下两个优点：

去掉括号后表达式无歧义，上式即便写成 1 2 + 3 4 + * 也可以依据次序计算出正确结果。 适合用栈操作运算：遇到数字则入栈；遇到算符则取出栈顶两个数字进行计算，并将结果压入栈中

# 2、思路

  • 这道题的思路很简单，就是遇到数字就压入栈，遇到字符就取出栈顶两个数字进行运算，再压入栈
  • 要注意的是我们给的数据其实是一个字符型指针数组，里面存放的都是指针，这些指针再指向字符串
  • 具体实现细节看代码

# 3、代码

int evalRPN(char ** tokens, int tokensSize){
    int stack[tokensSize];
    int stackTop =0;
    for (int i=0;i< tokensSize;i++)
    {
        //tokens是字符型指针数组，里面存放的都是指针，这些指针再指向字符串
        char* token = tokens[i];
        //判断是否是算术符，不是则将字符转化为int型整数 atoi()
        if((token[0] >= '0' && token[0]<= '9') || strlen(token) >1){
           stack[stackTop++] = atoi(token); 
        }
        else {
            switch(token[0])
            {
                case'+':
                    stack[stackTop -2] = stack[stackTop -2] + stack[stackTop-1];
                    break;
                case'-':
                    stack[stackTop -2] = stack[stackTop -2] - stack[stackTop-1];
                    break;
                case'*':
                    stack[stackTop -2] = stack[stackTop -2] * stack[stackTop-1];
                    break;
                case'/':
                    stack[stackTop -2] = stack[stackTop -2] / stack[stackTop-1];
                    break;
             }
             stackTop--;
        }
    }
    return stack[stackTop -1];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

# 六、滑动窗口最大值

239. 滑动窗口最大值 - 力扣（LeetCode） (opens new window)

# 1、题目

给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回 滑动窗口中的最大值 。

示例 1：

输入：nums = [1,3,-1,-3,5,3,6,7], k = 3
输出：[3,3,5,5,6,7]
解释：
滑动窗口的位置                最大值

---------------               -----

[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7
    
    
示例 2：

输入：nums = [1], k = 1
输出：[1]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

提示：

1 <= nums.length <= 105 -10^4 <= nums[i] <= 10^4 1 <= k <= nums.length

# 2、思路

  • 我们需要一个队列，这个队列呢，放进去窗口里的元素，然后随着窗口的移动，队列也一进一出，每次移动之后，队列告诉我们里面的最大值是什么

  • 每次窗口移动的时候，调用que.pop(滑动窗口中移除元素的数值)，que.push(滑动窗口添加元素的数值)，然后que.front()就返回我们要的最大值。

  • 这么个队列香不香，要是有现成的这种数据结构是不是更香了！

  • 可惜了，没有！ 我们需要自己实现这么个队列。

  • 其实队列没有必要维护窗口里的所有元素，只需要维护有可能成为窗口里最大值的元素就可以了，同时保证队列里的元素数值是由大到小的。

  • 那么这个维护元素单调递减的队列就叫做单调队列，即单调递减或单调递增的队列。C++中没有直接支持单调队列，需要我们自己来实现一个单调队列

  • 不要以为实现的单调队列就是 对窗口里面的数进行排序，如果排序的话，那和优先级队列又有什么区别了呢。

239.滑动窗口最大值

  • 对于窗口里的元素{2, 3, 5, 1 ,4}，单调队列里只维护{5, 4} 就够了，保持单调队列里单调递减，此时队列出口元素就是窗口里最大元素。

  • 此时大家应该怀疑单调队列里维护着{5, 4} 怎么配合窗口进行滑动呢？

  • 设计单调队列的时候，pop，和push操作要保持如下规则：

    • pop(value)：如果窗口移除的元素value等于单调队列的出口元素（队首），那么队列弹出元素，否则不用任何操作
    • push(value)：如果push的元素value大于入口元素(队尾)的数值，那么就将队列入口的元素弹出，直到push元素的数值小于等于队列入口元素的数值为止

  • 保持如上规则，每次窗口移动的时候，只要问que.front()就可以返回当前窗口的最大值。

# 3、代码

int* maxSlidingWindow(int* nums, int numsSize, int k, int* returnSize){
    int resultSize = numsSize - k + 1;
    int* result = (int *)malloc(sizeof(int) * resultSize);
    * returnSize = resultSize;
    int queue[numsSize+1];
    int front=0,rear=0;
    int index=0;
    //初始化窗口的处理
    for(int i =0;i<k;i++){
        while(rear > front && nums[i] > queue[rear-1]){
            rear--;
        }
        queue[rear++] = nums[i];
    }
 	//将初始化窗口中最大的元素加进结果数组
    result[index++] = queue[front];
    
    //滑动窗口时的处理
    for(int i =k;i<numsSize;i++){
        //窗口滑动，（出队）
        if(queue[front] ==nums[i-k]){
            front++;
        }
        //进队处理
        while(rear > front && nums[i] > queue[rear-1]){
            //如果比队尾元素大，就要从队尾弹出
            rear--;
        }
        queue[rear++] = nums[i];
       
        result[index++] = queue[front];
    }
    return result;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

# 七、🧨前 K 个高频元素

# 1、题目

给你一个整数数组 nums 和一个整数 k ，请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。

示例 1:

输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]
示例 2:

输入: nums = [1], k = 1
输出: [1]
1
2
3
4
5
6
7
8

提示：

1 <= nums.length <= 105 k 的取值范围是 [1, 数组中不相同的元素的个数] 题目数据保证答案唯一，换句话说，数组中前 k 个高频元素的集合是唯一的

进阶：你所设计算法的时间复杂度 必须 优于 O(n log n) ，其中 n 是数组大小。

# 2、思路

  • 整个这个还没写，涉及了哈希表，和根堆，我先跳过了😥
编辑 (opens new window)
上次更新: 2023/09/13, 12:29:52
数组
二叉树(上)

← 二叉树(上)→

最近更新
01
51单片机及补充知识
09-13
02
独立按键
09-13
03
LCD1602液晶显示器
09-13
更多文章>
Theme by Vdoing | Copyright © 2019-2023 Evan Xu | MIT License