回溯算法（上）

1、回溯算法理论基础

代码随想录 (programmercarl.com) (opens new window)

回溯法模板：

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

2、组合问题

1、题目

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

示例 1：

输入：n = 4, k = 2
输出：
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]
    
示例 2：

输入：n = 1, k = 1
输出：[[1]]

提示：

• 1 <= n <= 20
• 1 <= k <= n

2、思路

2.1 暴力解法

• 直接的解法当然是使用for循环，例如示例中k为2，很容易想到 用两个for循环，这样就可以输出 和示例中一样的结果。

int n = 4;
for (int i = 1; i <= n; i++) {
    for (int j = i + 1; j <= n; j++) {
        cout << i << " " << j << endl;
    }
}

输入：n = 100, k = 3 那么就三层for循环，代码如下：

int n = 100;
for (int i = 1; i <= n; i++) {
    for (int j = i + 1; j <= n; j++) {
        for (int u = j + 1; u <= n; n++) {
            cout << i << " " << j << " " << u << endl;
        }
    }
}

• 如果n为100，k为50呢，那就50层for循环，是不是开始窒息，所以要用回溯法

2. 2 回溯法

• 回溯法解决的问题都可以抽象为树形结构（N叉树），用树形结构来理解回溯就容易多了。

• 把组合问题抽象为如下树形结构：

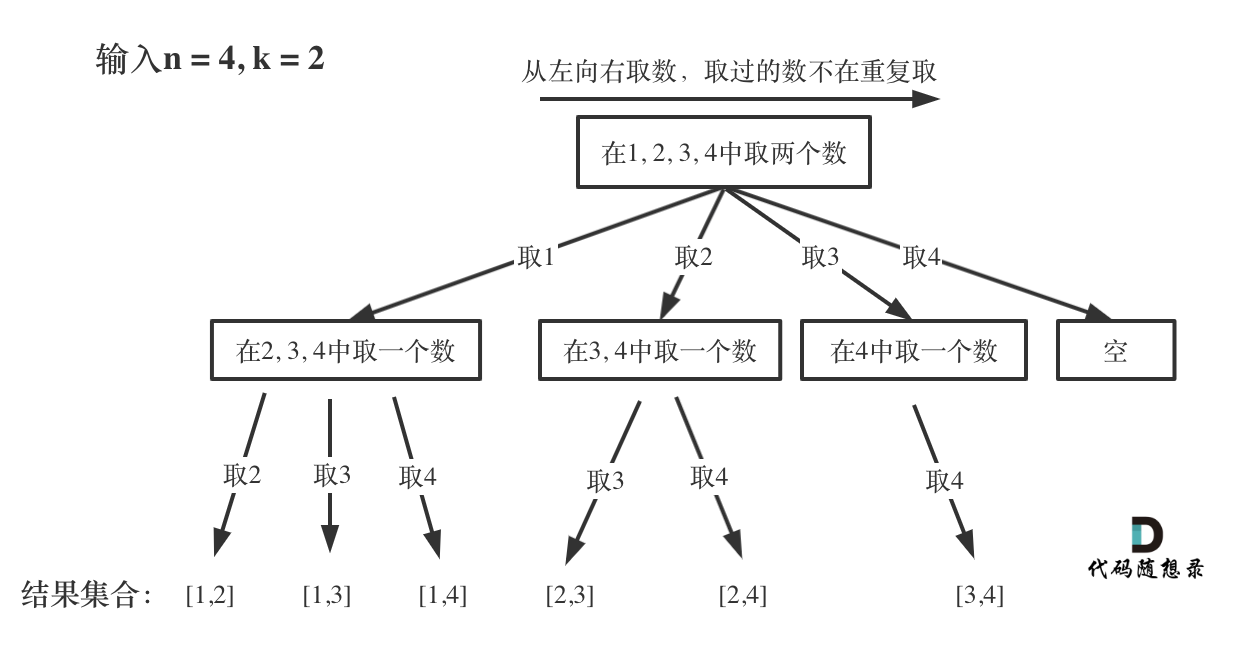
• 可以看出这棵树，一开始集合是 1，2，3，4， 从左向右取数，取过的数，不再重复取。

• 第一次取1，集合变为2，3，4 ，因为k为2，我们只需要再取一个数就可以了，分别取2，3，4，得到集合[1,2] [1,3] [1,4]，以此类推。

• 每次从集合中选取元素，可选择的范围随着选择的进行而收缩，调整可选择的范围。

• 图中可以发现n相当于树的宽度，k相当于树的深度。

• 那么如何在这个树上遍历，然后收集到我们要的结果集呢？

  • 图中每次搜索到了叶子节点，我们就找到了一个结果。
  • 相当于只需要把达到叶子节点的结果收集起来，就可以求得 n个数中k个数的组合集合。

• 单层搜索的过程
  • 回溯法的搜索过程就是一个树型结构的遍历过程，在如下图中，可以看出for循环用来横向遍历，递归的过程是纵向遍历。

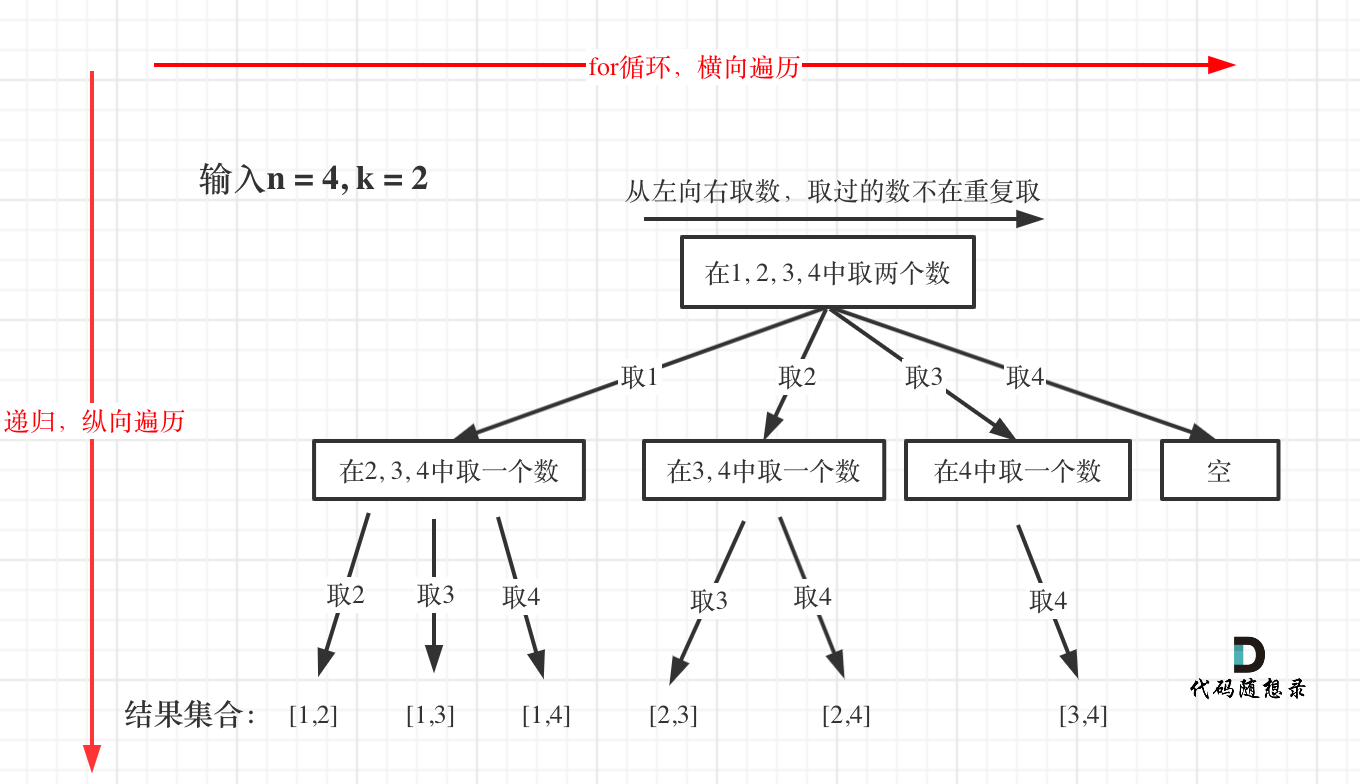
3、代码

/**
 * Return an array of arrays of size *returnSize.
 * The sizes of the arrays are returned as *returnColumnSizes array.
 * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
 */

int** result; //做为返回值返回的二维数组
int resultTop; //记录数量
int *path ; // 遍历路径
int pathTop; //记录已遍历路径数目

void backtracking(int n,int k, int stratIndex){
    //当path 中的元素为k时，将path数组放入 result 数组中
    if(pathTop == k){
        //path数组为我们动态申请，若直接将其地址放入二维数组，path数组中的值会随着我们回溯而逐渐变化
        //因此创建新的数组存储path中的值
        int * temp =(int* )malloc(sizeof(int)*k);
        for(int i =0;i<k;i++){
            temp[i] = path[i];
        }
        result[resultTop++] = temp;
        return ;
    }
    // for循环控制宽度，回溯函数为深度
    for(int i = stratIndex; i <= n ; i++ ){
        path[pathTop++] = i;
        backtracking(n , k , i + 1);
        pathTop--;
    }
}

int** combine(int n, int k, int* returnSize, int** returnColumnSizes){
    // path 数组存储符合条件的结果
    path = (int*)malloc(sizeof(int)*k);
    // result 二维数组存储符合条件的结果数组的集合（数组足够大，避免极端情况）
    result = (int ** )malloc(sizeof(int*)*10000);
    resultTop = pathTop = 0;

    // 回溯算法
    backtracking(n,k,1);

    *returnSize = resultTop;
    *returnColumnSizes = (int*) malloc(sizeof(int)*(*returnSize));
    for(int i = 0;i < (*returnSize);i++){
        (*returnColumnSizes)[i] = k;
    }
    return result;
}

4、剪枝优化

• 来举一个例子，n = 4，k = 4的话，那么第一层for循环的时候，从元素2开始的遍历都没有意义了。 在第二层for循环，从元素3开始的遍历都没有意义了。

• 这么说有点抽象，如图所示：

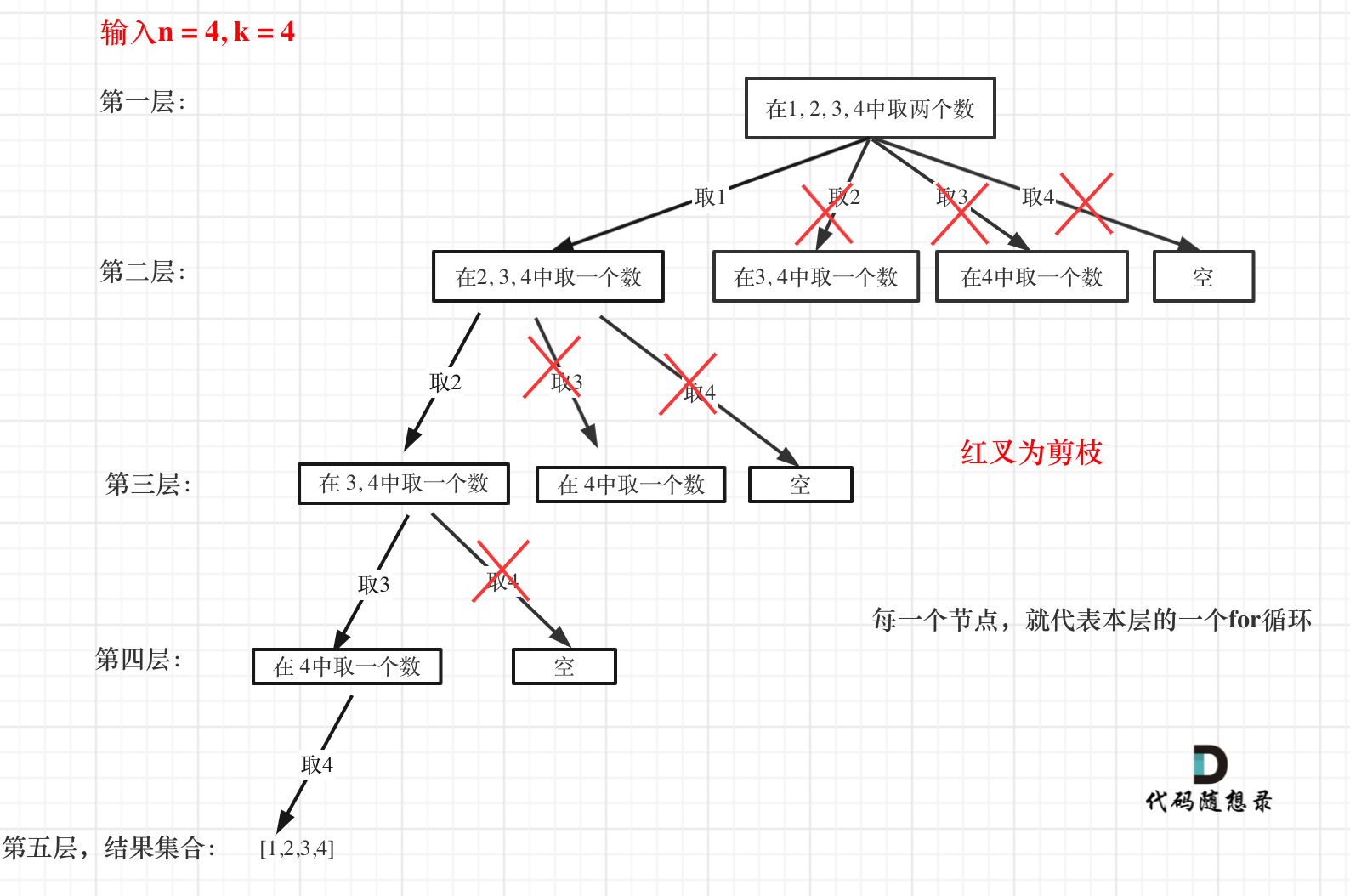
• 图中每一个节点（图中为矩形），就代表本层的一个for循环，那么每一层的for循环从第二个数开始遍历的话，都没有意义，都是无效遍历。

  所以，可以剪枝的地方就在递归中每一层的for循环所选择的起始位置。

  如果for循环选择的起始位置之后的元素个数 已经不足 我们需要的元素个数了，那么就没有必要搜索了。

• 注意代码中i，就是for循环里选择的起始位置。

  for (int i = startIndex; i <= n; i++) {
  

  接下来看一下优化过程如下：

  1. 已经选择的元素个数：path.size();
  2. 还需要的元素个数为: k - path.size();
  3. 在集合n中至多要从该起始位置 : n - (k - path.size()) + 1，开始遍历

• 为什么有个+1呢，因为包括起始位置，我们要是一个左闭的集合。

  • 举个例子，n = 4，k = 3， 目前已经选取的元素为0（path.size为0），n - (k - 0) + 1 即 4 - ( 3 - 0) + 1 = 2。
  • 从2开始搜索都是合理的，可以是组合[2, 3, 4]。
  • 这里大家想不懂的话，建议也举一个例子，就知道是不是要+1了。
  • 所以优化之后的for循环是：

  for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) // i为本次搜索的起始位置
  

3、组合总和III

1、题目

找出所有相加之和为 n 的 k 个数的组合，且满足下列条件：

• 只使用数字1到9
• 每个数字 最多使用一次

返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次，组合可以以任何顺序返回。

示例 1:

输入: k = 3, n = 7
输出: [[1,2,4]]
解释:
1 + 2 + 4 = 7
没有其他符合的组合了。

示例 2:

输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]
解释:
1 + 2 + 6 = 9
1 + 3 + 5 = 9
2 + 3 + 4 = 9
没有其他符合的组合了。

示例 3:

输入: k = 4, n = 1
输出: []
解释: 不存在有效的组合。
在[1,9]范围内使用4个不同的数字，我们可以得到的最小和是1+2+3+4 = 10，因为10 > 1，没有有效的组合。

• 提示:
  • 2 <= k <= 9
  • 1 <= n <= 60

2、思路

• 思路与上题基本一致（不多说）

3、代码

/**
 * Return an array of arrays of size *returnSize.
 * The sizes of the arrays are returned as *returnColumnSizes array.
 * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
 */

int **result;
int * path;
int resultTop;
int pathTop;

void backtracking(int n,int k ,int stratIndex,int sum){
    if(pathTop == k){
        if(sum == n){
        //path数组为我们动态申请，若直接将其地址放入二维数组，path数组中的值会随着我们回溯而逐渐变化
        //因此创建新的数组存储path中的值
        int* temp = (int*)malloc(sizeof(int)*k); 
        for(int i=0;i<k;i++){
            temp[i]= path[i];
        }
        result[resultTop++] = temp;
        return ;
        }
        return ;
    }
    
    // for循环控制宽度，回溯函数为深度
    for(int i=stratIndex;i<= 9;i++){
        path[pathTop++] = i;
        sum += i;
        // 下一次起始位就加一
        backtracking(n,k,i+1,sum);
        sum -= i;
        pathTop--;
    }

}

int** combinationSum3(int k, int n, int* returnSize, int** returnColumnSizes){
    
    //初始化辅助变量
    result = (int **)malloc(sizeof(int*)* 10000);
    path = (int *)malloc(sizeof(int) * k);
    pathTop = resultTop =0; 

    backtracking(n,k,1,0);

    *returnSize = resultTop;
    * returnColumnSizes = (int*)malloc(sizeof(int)* resultTop);
    for(int i=0;i<(*returnSize);i++){
        (*returnColumnSizes)[i] = k; 
    }
    return result;
}

• 剪枝优化也相同，都是把for循环判断语句改为：

   for(int i=stratIndex;i<= 9- (k - pathTop) + 1;i++){
  

4、电话号码字母组合

17. 电话号码的字母组合 - 力扣（LeetCode） (opens new window)

1、题目

• 给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。

• 给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

  

  示例 1：
  输入：digits = "23"
  输出：["ad","ae","af","bd","be","bf","cd","ce","cf"]
      
  示例 2：
  输入：digits = ""
  输出：[]
      
  示例 3：
  输入：digits = "2"
  输出：["a","b","c"]
  

• 提示：

  • 0 <= digits.length <= 4
  • digits[i] 是范围 ['2', '9'] 的一个数字。

2、思路

• 本题主要解决下面三个问题：
  • 数字和字母如何映射
  • 两个字母就两个for循环，三个字符我就三个for循环，以此类推，然后发现代码根本写不出来
  • 输入1 * #按键等等异常情况

2.1 映射解决

• 使用map或者定义一个二维数组，例如：string letterMap[10]，来做映射，我这里定义一个二维数组，代码如下：

const string letterMap[10] = {
    "", // 0
    "", // 1
    "abc", // 2
    "def", // 3
    "ghi", // 4
    "jkl", // 5
    "mno", // 6
    "pqrs", // 7
    "tuv", // 8
    "wxyz", // 9
};

2.2 回溯解决n个循环

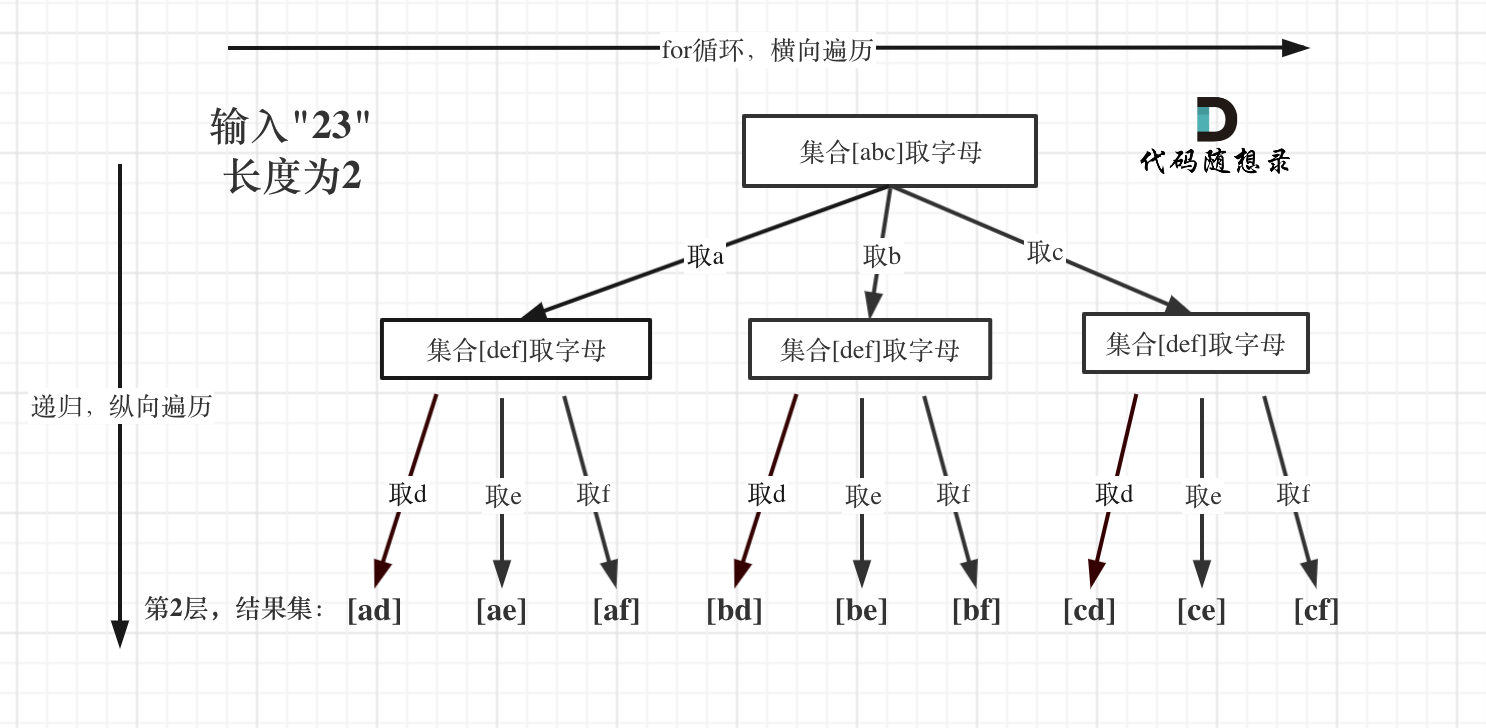
• digits 的长度作为回溯的深度，映射里对应的字符串的长度为长度

2.3 异常情况

• 注意：输入1 * #按键等等异常情况
• 代码中最好考虑这些异常情况，但题目的测试数据中应该没有异常情况的数据，所以我就没有加了。

3、代码

char* path;
int pathTop;
char** result;
int resultTop;
char* letterMap[10] = {"", //0
        "", //1
        "abc", //2
        "def", //3
        "ghi", //4
        "jkl", //5
        "mno", //6
        "pqrs", //7
        "tuv", //8
        "wxyz", //9
};
void backTracking(char* digits,int index){
    if(index== strlen(digits)){
        //最后要添加一个0（结束符），所以要加一
        char * temp = (char*)malloc(sizeof(char)* index+1);
        for(int i=0; i< index;i++){
            temp[i] = path[i]; 
        }
        // 因为是字符数组，所以要在后面加一个 0 ，表示结束
        temp[index] =0;
        result[resultTop++] = temp;
        return;
    }

    //将字符数字转换为真的数字
    int digit = digits[index] - '0';//每次取出对应数字，给下面映射使用
    //找到letterMap中对应的字符串
    char* letters = letterMap[digit];  
    for(int i=0;i<strlen(letters);i++){
        path[pathTop++] = letters[i];
        backTracking(digits,index+1);
        pathTop--;
    }
}


char ** letterCombinations(char * digits, int* returnSize){
    path = (char *)malloc(sizeof(char)*strlen(digits));
    result = (char**)malloc(sizeof(char*)* 10000);
    * returnSize = 0;

    if(strlen(digits) == 0 ){
        return result;
    }
    pathTop = resultTop =0;
    backTracking(digits,0);
    * returnSize = resultTop;
    return result;
}

5、组合总和

39. 组合总和 - 力扣（LeetCode） (opens new window)

1、题目

• 给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。

• candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。

  对于给定的输入，保证和为 target 的不同组合数少于 150 个。

示例 1：
输入：candidates = [2,3,6,7], target = 7
输出：[[2,2,3],[7]]
解释：
	- 2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意 2 可以使用多次。
	- 7 也是一个候选， 7 = 7 。
	- 仅有这两种组合。
    
    
示例 2：
输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]

示例 3：
输入: candidates = [2], target = 1
输出: []

• 提示：
  • 1 <= candidates.length <= 30
  • 2 <= candidates[i] <= 40
  • candidates 的所有元素 互不相同
  • 1 <= target <= 40

2、思路

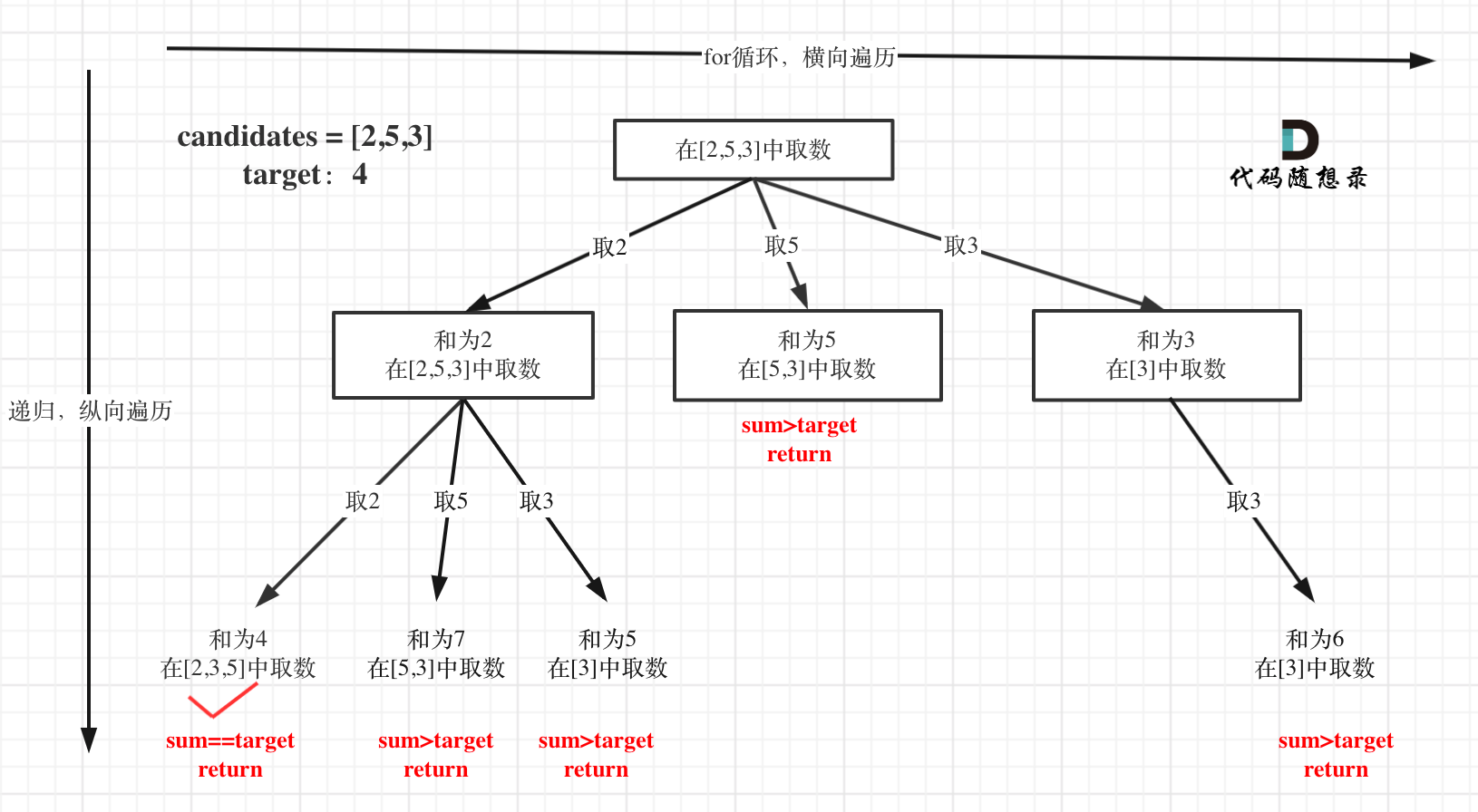
• 抽象树的宽度由 candidates 数组的长度决定，深度则根据 target 变化

3、代码

int **result;
int resultTop;
int *path;
int pathTop;
int *length;

void backTracking(int target,int index,int * candidates, int candidatesSize,int sum){
    if(sum >= target){
        if(sum == target){
            int* temp = (int*)malloc(sizeof(int)* pathTop);
            for(int i=0 ;i < pathTop; i++){
              temp[i] = path[i];
            }
        length[resultTop] = pathTop;
        result[resultTop++] = temp;
        
    }
        return ; 
    }
   
    // i的起始为index，这样就不会出现数字相同，但顺序不相同的情况
    for(int i = index; i < candidatesSize; i++ ){
        path[pathTop++] = candidates[i];
        sum += candidates[i];
        backTracking(target,i,candidates,candidatesSize,sum);
        sum -= candidates[i];
        pathTop--;
    }

}


int** combinationSum(int* candidates, int candidatesSize, int target, int* returnSize, int** returnColumnSizes){
    result = (int **)malloc(sizeof(int*)*151);
    path = (int*)malloc(sizeof(int)*target);
    length = (int*)malloc(sizeof(int)*200);
    resultTop = pathTop = 0;

    backTracking(target,0,candidates,candidatesSize,0);

    * returnSize = resultTop;
    * returnColumnSizes = (int* )malloc(sizeof(int)*resultTop);
    for(int i=0;i<resultTop;i++){
        (*returnColumnSizes)[i] = length[i];
    }
    return result;
}

6、组合总和II

40. 组合总和 II - 力扣（LeetCode） (opens new window)

1、题目

• 给定一个候选人编号的集合 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。
• candidates 中的每个数字在每个组合中只能使用 一次 。
• 注意：解集不能包含重复的组合。

示例 1:

输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]

示例 2:
输入: candidates = [2,5,2,1,2], target = 5,
输出:
[
[1,2,2],
[5]
]
 

• 提示 :

  1 <= candidates.length <= 100 1 <= candidates[i] <= 50 1 <= target <= 30

2、思路

• 这道题目和39.组合总和 (opens new window) (opens new window)如下区别：
  1. 本题candidates 中的每个数字在每个组合中只能使用一次。
  2. 本题数组candidates的元素是有重复的，而39.组合总和 (opens new window) (opens new window)是无重复元素的数组candidates

• 主要的难点在于区别2中：集合（数组candidates）有重复元素，但还不能有重复的组合。

  • 如：[2,1,2]，[1,2,2] 这种情况是不可以的

• 要解决这个问题我们就要对数组进行排序，然后在for循环里进行判断（因为我们要的是树层去重），如果当前遍历下标对应的元素与上一次遍历的元素相同，那么跳过该层遍历。

3、代码

/**
 * Return an array of arrays of size *returnSize.
 * The sizes of the arrays are returned as *returnColumnSizes array.
 * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
 */

int ** result;
int resultTop;
int * path;
int pathTop;
int * lengths;
int cmp(const void* a1, const void* a2) {
    return *((int*)a1) - *((int*)a2);
}

void backtracking(int* candidates, int candidatesSize, int target,int sum,int index){
    if(sum >= target){
        if(sum == target){
            int* temp = (int*)malloc(sizeof(int)* pathTop);
            for(int i=0;i<pathTop;i++){
                temp[i] = path[i];
            }
            result[resultTop] = temp;
            lengths[resultTop++] = pathTop; 
        }
        return ;
    }

    for(int i = index;i < candidatesSize;i++){
        //对同一层树中使用过的元素跳过
        if(i > index && candidates[i] == candidates[i-1])
            {continue;}
        sum += candidates[i];
        path[pathTop++] = candidates[i];
        backtracking(candidates,candidatesSize,target,sum,i+1);
        pathTop--;
        sum -= candidates[i];
    }
}
 
int** combinationSum2(int* candidates, int candidatesSize, int target, int* returnSize, int** returnColumnSizes){

    result = (int **)malloc(sizeof(int*)*100);
    path = (int *)malloc(sizeof(int)* target);
    lengths = (int*)malloc(sizeof(int)* 100);
    resultTop = pathTop = 0;

    //快速排序candidates，让相同元素挨到一起
    qsort(candidates, candidatesSize, sizeof(int), cmp);

    backtracking(candidates,candidatesSize,target,0,0);
    
    * returnSize = resultTop;
    * returnColumnSizes = (int*)malloc(sizeof(int)* (*returnSize));
    for(int i=0;i<(*returnSize);i++){
       (* returnColumnSizes)[i] = lengths[i];
    }
    
    return result;

}

7、分割回文串

1、题目

• 给你一个字符串 s，请你将 s 分割成一些子串，使每个子串都是 回文串 。返回 s 所有可能的分割方案。
• 回文串 是正着读和反着读都一样的字符串。

示例 1：
输入：s = "aab"
输出：[["a","a","b"],["aa","b"]]

示例 2：
输入：s = "a"
输出：[["a"]]

• 提示：
  • 1 <= s.length <= 16
  • s 仅由小写英文字母组成

2、思路

3、代码

/**
 * Return an array of arrays of size *returnSize.
 * The sizes of the arrays are returned as *returnColumnSizes array.
 * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
 */
char** path;
int pathTop;
char*** ans;
int ansTop = 0;
int* ansSize;

//将path中的字符串全部复制到ans中
void copy() {
    //创建一个临时tempPath保存path中的字符串
    char** tempPath = (char**)malloc(sizeof(char*) * pathTop);
    int i;
    for(i = 0; i < pathTop; i++) {
        tempPath[i] = path[i];
    }
    //保存tempPath
    ans[ansTop] = tempPath;
    //将当前path的长度（pathTop）保存在ansSize中
    ansSize[ansTop++] = pathTop;
}

//判断字符串是否为回文字符串
bool isPalindrome(char* str, int startIndex, int endIndex) {
    //双指针法：当endIndex（右指针）的值比startIndex（左指针）大时进行遍历
    while(endIndex >= startIndex) {
        //若左指针和右指针指向元素不一样，返回False
        if(str[endIndex--] != str[startIndex++])
            return 0;
    }
    return 1;
}

//切割从startIndex到endIndex子字符串
char* cutString(char* str, int startIndex, int endIndex) {
    //开辟字符串的空间
    char* tempString = (char*)malloc(sizeof(char) * (endIndex - startIndex + 2));
    int i;
    int index = 0;
    //复制子字符串
    for(i = startIndex; i <= endIndex; i++)
        tempString[index++] = str[i];
    //用'\0'作为字符串结尾
    tempString[index] = '\0';
    return tempString;
}

void backTracking(char* str, int strLen,  int startIndex) {
    if(startIndex >= strLen) {
        //将path拷贝到ans中
        copy();
        return ;
    }

    int i;
    for(i = startIndex; i < strLen; i++) {
        //若从subString到i的子串是回文字符串，将其放入path中
        if(isPalindrome(str, startIndex, i)) {
            path[pathTop++] = cutString(str, startIndex, i);
        }
        //若从startIndex到i的子串不为回文字符串，跳过这一层 
        else {
            continue;
        }
        //递归判断下一层
        backTracking(str, strLen, i + 1);
        //回溯，将path中最后一位元素弹出
        pathTop--;
    }
}

char*** partition(char* s, int* returnSize, int** returnColumnSizes){
    int strLen = strlen(s);
    //因为path中的字符串最多为strLen个（即单个字符的回文字符串），所以开辟strLen个char*空间
    path = (char**)malloc(sizeof(char*) * strLen);
    //存放path中的数组结果
    ans = (char***)malloc(sizeof(char**) * 40000);
    //存放ans数组中每一个char**数组的长度
    ansSize = (int*)malloc(sizeof(int) * 40000);
    ansTop = pathTop = 0;

    //回溯函数
    backTracking(s, strLen, 0);

    //将ansTop设置为ans数组的长度
    *returnSize = ansTop;
    //设置ans数组中每一个数组的长度
    *returnColumnSizes = (int*)malloc(sizeof(int) * ansTop);
    int i;
    for(i = 0; i < ansTop; ++i) {
        (*returnColumnSizes)[i] = ansSize[i];
    }
    return ans;
}

8、复原IP地址

93. 复原 IP 地址 - 力扣（LeetCode） (opens new window)

1、题目

• 有效 IP 地址 正好由四个整数（每个整数位于 0 到 255 之间组成，且不能含有前导 0），整数之间用 '.' 分隔。
  • 例如："0.1.2.201" 和 "192.168.1.1" 是 有效 IP 地址
  • 但是 "0.011.255.245"、"192.168.1.312" 和 "192.168@1.1" 是 无效 IP 地址。
• 给定一个只包含数字的字符串 s ，用以表示一个 IP 地址，返回所有可能的有效 IP 地址，这些地址可以通过在 s 中插入 '.' 来形成。你 不能 重新排序或删除 s 中的任何数字。你可以按 任何顺序返回答案。

示例 1：
输入：s = "25525511135"
输出：["255.255.11.135","255.255.111.35"]
    
示例 2：
输入：s = "0000"
输出：["0.0.0.0"]
    
示例 3：
输入：s = "101023"
输出：["1.0.10.23","1.0.102.3","10.1.0.23","10.10.2.3","101.0.2.3"]

• 提示：
  • 1 <= s.length <= 20
  • s 仅由数字组成

2、思路

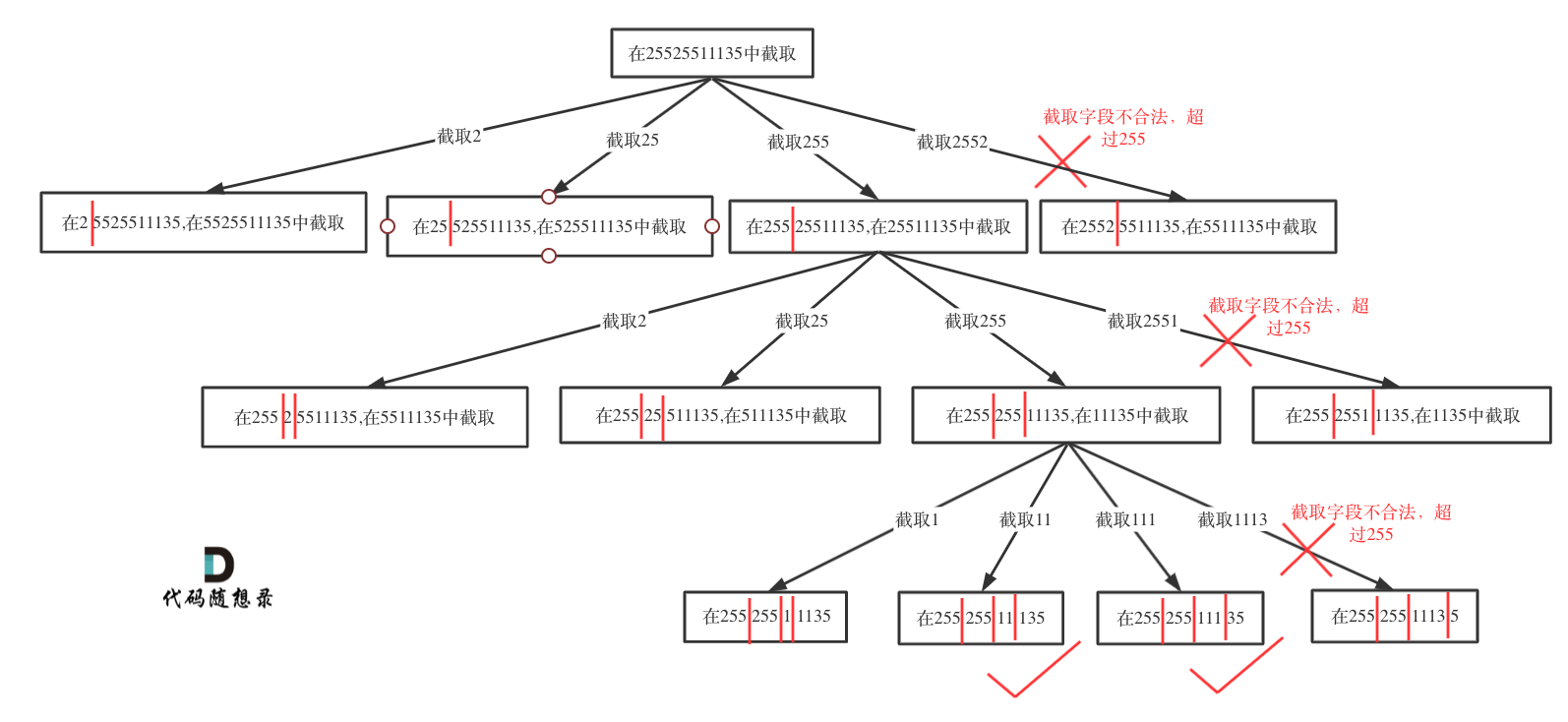
3、代码

// 记录结果
char ** result;
int resultTop;

//记录应该加入'.'的位置
int segments[3];
// 判断加入字符是否合法
int isValid(char* s,int start,int end){
    if(start > end){
        return 0;
    }
    if(s[start] == '0' && start != end){
        return false;
    }
    int num =0;
    for(int i = start;i <= end;i++){
        // 判断是否出现非法字符
        if(s[i] > '9' || s[i] < '0'){
            return false;
        }
        num = num * 10 + (s[i] - '0');
        //如果大于255了不合法
        if(num > 255){ 
            return false;
        }
    }
    return true;
}


//startIndex为起始搜索位置，pointNum为'.'对象
void backTracking(char* s, int startIndex, int pointNum) {
    //若'.'数量为3，分隔结束
    if(pointNum == 3) {
        //若最后一段字符串符合要求，将当前的字符串放入result种
        if(isValid(s, startIndex, strlen(s) - 1)) {
            char* tempString = (char*)malloc(sizeof(char) * strlen(s) + 4);
            int j;
            //记录添加字符时tempString的下标
            int count = 0;
            //记录添加字符时'.'的使用数量
            int count1 = 0;
            for(j = 0; j < strlen(s); j++) {
                tempString[count++] = s[j];
                //若'.'的使用数量小于3且当前下标等于'.'下标，添加'.'到数组
                if(count1 < 3 && j == segments[count1]) {
                    tempString[count++] = '.';
                    count1++;
                }
            }
            tempString[count] = 0;
            //扩容result数组
            result = (char**)realloc(result, sizeof(char*) * (resultTop + 1));
            result[resultTop++] = tempString;
        }
        return ;
    }

    int i;
    for(i = startIndex; i < strlen(s); i++) {
        if(isValid(s, startIndex, i)) {
            //记录应该添加'.'的位置
            segments[pointNum] = i;
            backTracking(s, i + 1, pointNum + 1);
        }
        else {
            break;
        }
    }
}

char ** restoreIpAddresses(char * s, int* returnSize){
    result =(char**)malloc(0);
    resultTop = 0;
    backTracking(s,0,0);
    *returnSize = resultTop;
    return result;
}

9、子集

78. 子集 - 力扣（LeetCode） (opens new window)

1、题目

• 给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。
• 解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。

示例 1：
输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例 2：
输入：nums = [0]
输出：[[],[0]]

提示：

• 1 <= nums.length <= 10
• -10 <= nums[i] <= 10
• nums 中的所有元素 互不相同

2、思路

• 从图中红线部分，可以看出遍历这个树的时候，把所有节点都记录下来，就是要求的子集集合。

3、代码

int* path;
int pathTop;
int** ans;
int ansTop;
//记录二维数组中每个一维数组的长度
int* length;
//将当前path数组复制到ans中
void copy() {
    int* tempPath = (int*)malloc(sizeof(int) * pathTop);
    int i;
    for(i = 0; i < pathTop; i++) {
        tempPath[i] = path[i];
    }
    ans = (int**)realloc(ans, sizeof(int*) * (ansTop+1));
    length[ansTop] = pathTop;
    ans[ansTop++] = tempPath;
}

void backTracking(int* nums, int numsSize, int startIndex) {
    //收集子集，要放在终止添加的上面，否则会漏掉自己
    copy();
    //若startIndex大于数组大小，返回
    if(startIndex >= numsSize) {
        return;
    }
    int j;
    for(j = startIndex; j < numsSize; j++) {
        //将当前下标数字放入path中
        path[pathTop++] = nums[j];
        backTracking(nums, numsSize, j+1);
        //回溯
        pathTop--;
    }
}

int** subsets(int* nums, int numsSize, int* returnSize, int** returnColumnSizes){
    //初始化辅助变量
    path = (int*)malloc(sizeof(int) * numsSize);
    ans = (int**)malloc(0);
    length = (int*)malloc(sizeof(int) * 1500);
    ansTop = pathTop = 0;
    //进入回溯
    backTracking(nums, numsSize, 0);
    //设置二维数组中元素个数
    *returnSize = ansTop;
    //设置二维数组中每个一维数组的长度
    *returnColumnSizes = (int*)malloc(sizeof(int) * ansTop);
    int i;
    for(i = 0; i < ansTop; i++) {
        (*returnColumnSizes)[i] = length[i];
    }
    return ans;
}

10、子集II

90. 子集 II - 力扣（LeetCode） (opens new window)

1、题目

• 给你一个整数数组 nums ，其中可能包含重复元素，请你返回该数组所有可能的子集（幂集）。
• 解集 不能 包含重复的子集。返回的解集中，子集可以按 任意顺序 排列。

示例 1：
输入：nums = [1,2,2]
输出：[[],[1],[1,2],[1,2,2],[2],[2,2]]

示例 2：
输入：nums = [0]
输出：[[],[0]]

• 提示：
  • 1 <= nums.length <= 10
  • -10 <= nums[i] <= 10

2、思路

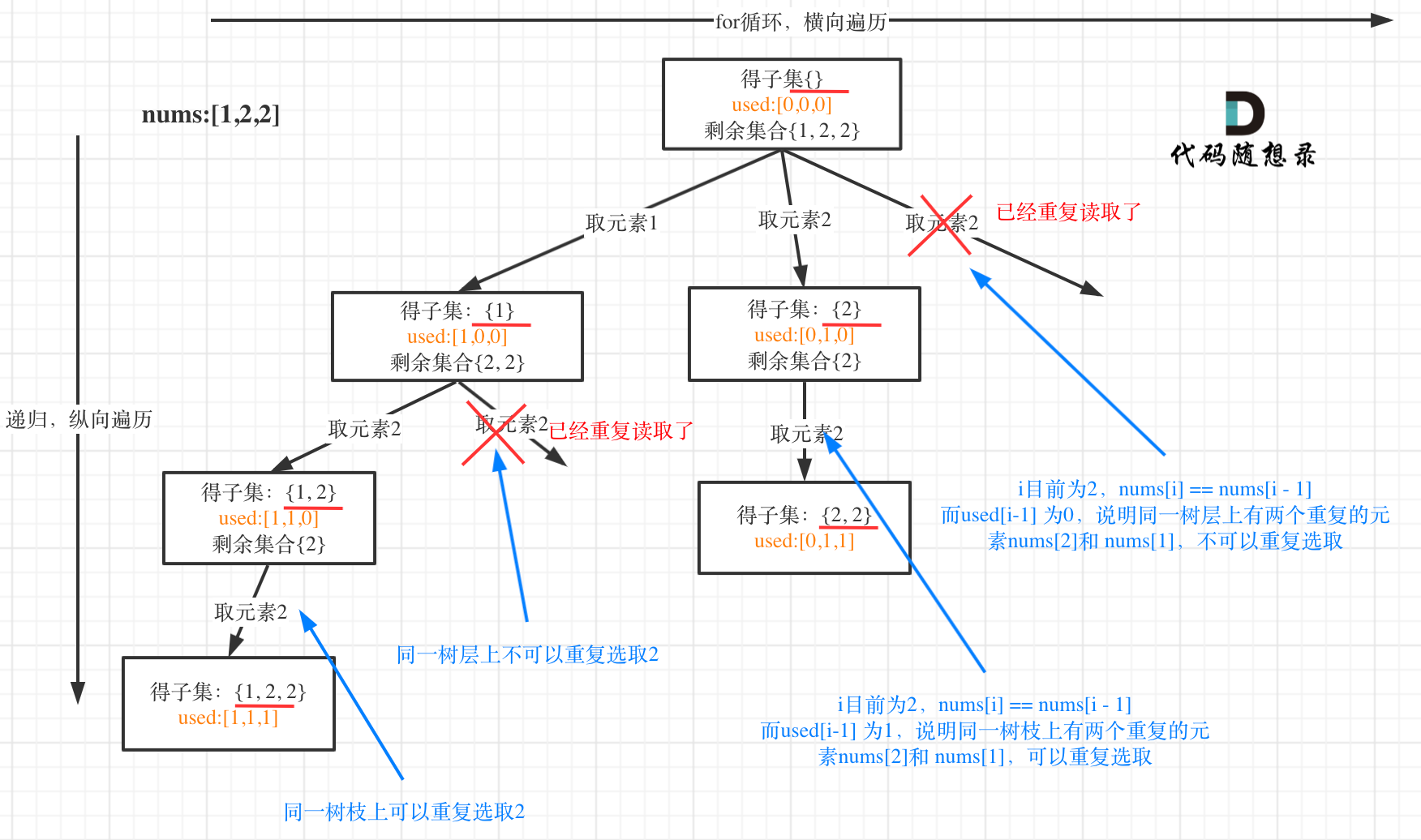
• 和 **9、子集 ** 对比，本题的区别在于给定我们的数组中的元素不再是唯一的，可能出现元素相同的情况，所以我们要通过排序再加"树层去重"来进行回溯

3、代码

/**
 * Return an array of arrays of size *returnSize.
 * The sizes of the arrays are returned as *returnColumnSizes array.
 * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
 */
int ** result;
int * path;
int resultTop;
int pathTop;
int* lengths;
int cmp(const void* a1, const void* a2) {
    return *((int*)a1) - *((int*)a2);
}
void copy(){
    int* temp = (int*)malloc(sizeof(int)* pathTop);
    for(int i=0; i< pathTop;i++){
        temp[i] = path[i];
    }
    result= (int**)realloc(result, sizeof(int*) * (resultTop+1));
    result[resultTop] = temp;
    lengths[resultTop++] = pathTop;
    return;
}

void backTracking(int *nums,int numsSize,int startIndex){
    copy();
    if(startIndex >= numsSize){
        return ;
    }

    for(int i =startIndex; i < numsSize; i++ ){
        // 同层去重
        if(i >startIndex && nums[i-1] == nums[i]){
            continue;
        }
        path[pathTop++] = nums[i];
        backTracking(nums,numsSize,i+1);
        pathTop--;
    }
}
 
int** subsetsWithDup(int* nums, int numsSize, int* returnSize, int** returnColumnSizes){
    
    result = (int**)malloc(0);
    path = (int*)malloc(sizeof(int)* numsSize);
    lengths = (int*) malloc(sizeof(int)* 1500);
    resultTop = pathTop = 0;
    //快速排序candidates，让相同元素挨到一起
    qsort(nums, numsSize, sizeof(int), cmp);
    backTracking(nums,numsSize,0);

    * returnSize = resultTop ;
    * returnColumnSizes = (int*)malloc(sizeof(int)* resultTop);
    for(int i=0; i < resultTop;i++){
        (*returnColumnSizes)[i] = lengths[i];
    }

    return result;
}

11、递增子序列

491. 递增子序列 - 力扣（LeetCode） (opens new window)

1、题目

• 给你一个整数数组 nums ，找出并返回所有该数组中不同的递增子序列，递增子序列中 至少有两个元素 。你可以按 任意顺序 返回答案。
• 数组中可能含有重复元素，如出现两个整数相等，也可以视作递增序列的一种特殊情况。

示例 1：
输入：nums = [4,6,7,7]
输出：[[4,6],[4,6,7],[4,6,7,7],[4,7],[4,7,7],[6,7],[6,7,7],[7,7]]
    
示例 2：
输入：nums = [4,4,3,2,1]
输出：[[4,4]]

• 提示：
  • 1 <= nums.length <= 15
  • -100 <= nums[i] <= 100

2、思路

• 这题我题目都没怎么看懂了😭，自己本来写了这样的代码：

/**
 * Return an array of arrays of size *returnSize.
 * The sizes of the arrays are returned as *returnColumnSizes array.
 * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
 */

int** result;
int *path;
int resultTop;
int pathTop;
int* lengths;

void copy(){
    int* temp = (int*)malloc(sizeof(int)* pathTop);
    for(int i=0;i < pathTop;i++){
        temp[i] = path[i];
    }

    result[resultTop] = temp;
    lengths[resultTop++] = pathTop;
    return ;
}

void backTracking(int * nums,int numsSize,int startIndex){
    if(pathTop > 1){
        copy();
    }
    if(pathTop > numsSize){
        return ;
    }

    for(int i= startIndex;i < numsSize ; i++){
        if( i > startIndex && nums[i-1] == nums[i]){
            continue;
        }
        if( pathTop>0 && path[pathTop-1] > nums[i]){
            continue;
        }
        path[pathTop++] = nums[i];
        backTracking(nums,numsSize,i+1);
        pathTop--;
    }
}



int** findSubsequences(int* nums, int numsSize, int* returnSize, int** returnColumnSizes){
    
    result = (int**)malloc(sizeof(int*)*33000);
    path = (int*)malloc(sizeof(int)* numsSize);
    lengths = (int*)malloc(sizeof(int)* 33000);
    resultTop = pathTop =0;
    backTracking(nums,numsSize,0);
    * returnSize = resultTop;
    * returnColumnSizes = (int*)malloc(sizeof(int)* resultTop);
    for(int i=0; i < resultTop;i++){
        (*returnColumnSizes)[i] = lengths[i];
    }
    return result;
}

• 但是执行 [1,2,3,4,5,6,7,8,9,10,1,1,1,1,1]测试例子时，就错误了，结果里面多出了 [1,1],[1,1,1],[1,1,1,1],[1,1,1,1,1]，这几个结果（我自己理解题目的话，也是有这几个答案的），因为我自己没怎么理解题目，所以就自己放随想录了题解了
• 代码随想录 (programmercarl.com) (opens new window)

12、全排列

46. 全排列 - 力扣（LeetCode） (opens new window)

1、题目

• 给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例 2：

输入：nums = [0,1]
输出：[[0,1],[1,0]]
示例 3：

输入：nums = [1]
输出：[[1]]

• 提示：
  • 1 <= nums.length <= 6
  • -10 <= nums[i] <= 10
  • nums 中的所有整数 互不相同

2、思路

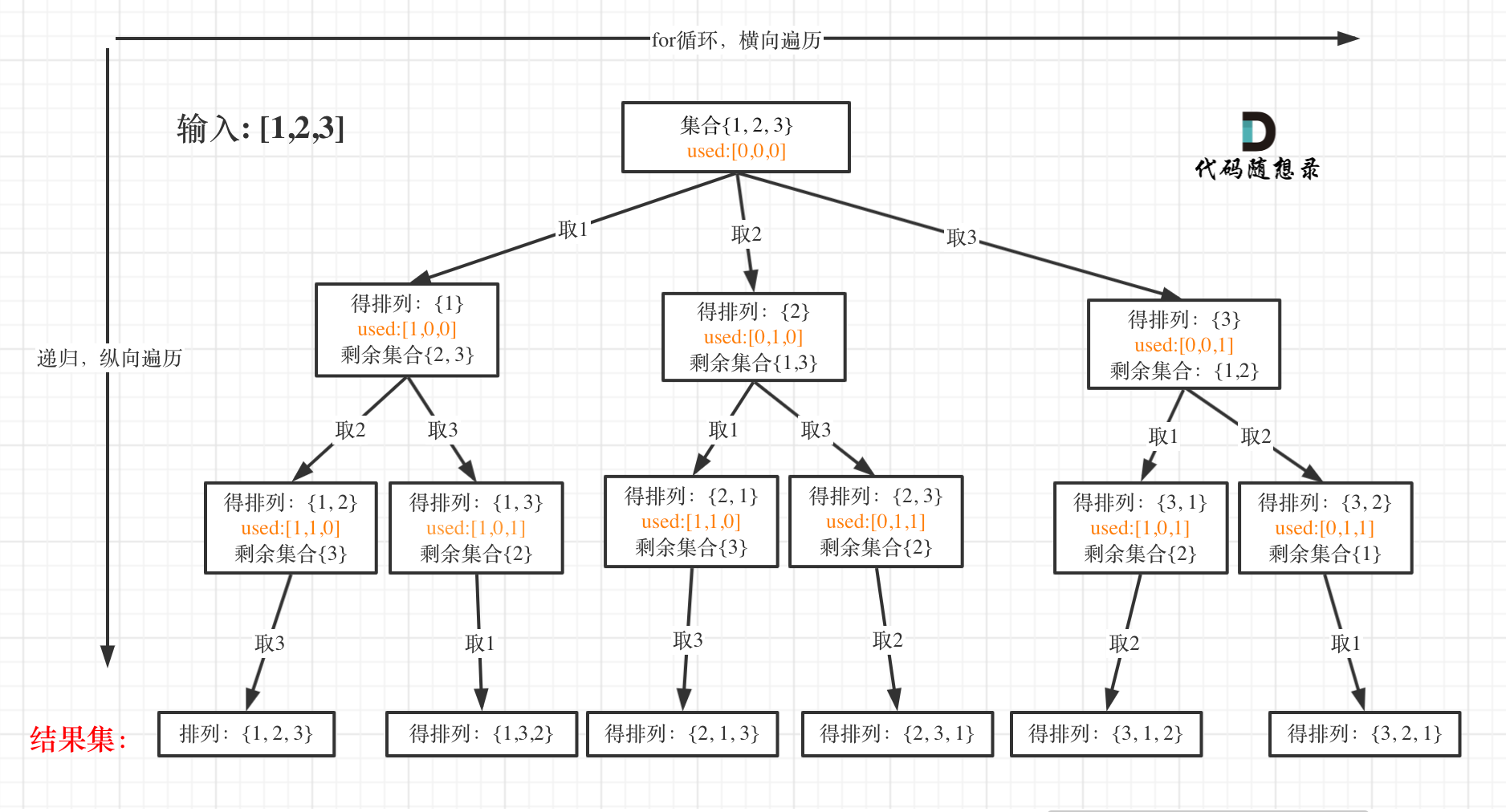
• 这题主要就是要判断元素是否被使用过，随想录是创建了一个数组按下标记录对应位置元素是否被使用，（我自己则是每次遍历元素都进行判断，查看元素是否在 path数组里，是说明被使用）

3、代码

• 下面这个是自己写的代码：

int** result;
int * path;
int pathTop;
int resultTop;
int * lengths;

void copy(){
    int* temp = (int*)malloc(sizeof(int)*pathTop);
    for(int i=0;i<pathTop;i++){
        temp[i] = path[i];
    }
    result[resultTop++] = temp;
    return ;
}

int find(int key){
    for(int i=0;i<pathTop;i++){
        if(key == path[i]){
            return 1;  //已使用
        }       
    }
    return 0;  //未被使用
}

void backTracking(int* nums, int numsSize){
    if(pathTop == numsSize){
        copy();
        return ;
    }
    for(int i =0;i<numsSize;i++){
        if(find(nums[i])){
            continue;
        }
        path[pathTop++] = nums[i];
        backTracking(nums,numsSize);
        pathTop--;
    }

}

int** permute(int* nums, int numsSize, int* returnSize, int** returnColumnSizes){
    result = (int**)malloc(sizeof(int*)*1000);
    path = (int *)malloc(sizeof(int)* numsSize);
    pathTop = resultTop =0;

    backTracking(nums,numsSize);

    *returnSize = resultTop;
    *returnColumnSizes = (int*)malloc(sizeof(int)*resultTop);
    for(int i =0 ;i<resultTop;i++){
        (*returnColumnSizes)[i]= numsSize;
    }
    return result;
}

• 看了随想录的，感觉比自己写的好😭

int* path;
int pathTop;
int** ans;
int ansTop;

//将used中元素都设置为0
void initialize(int* used, int usedLength) {
    int i;
    for(i = 0; i < usedLength; i++) {
        used[i] = 0;
    }
}

//将path中元素拷贝到ans中
void copy() {
    int* tempPath = (int*)malloc(sizeof(int) * pathTop);
    int i;
    for(i = 0; i < pathTop; i++) {
        tempPath[i] = path[i];
    }
    ans[ansTop++] = tempPath;
}

void backTracking(int* nums, int numsSize, int* used) {
    //若path中元素个数等于nums元素个数，将nums放入ans中
    if(pathTop == numsSize) {
        copy();
        return;
    }
    int i;
    for(i = 0; i < numsSize; i++) {
        //若当前下标中元素已使用过，则跳过当前元素
        if(used[i])
            continue;
        used[i] = 1;
        path[pathTop++] = nums[i];
        backTracking(nums, numsSize, used);
        //回溯
        pathTop--;
        used[i] = 0;
    }
}

int** permute(int* nums, int numsSize, int* returnSize, int** returnColumnSizes){
    //初始化辅助变量
    path = (int*)malloc(sizeof(int) * numsSize);
    ans = (int**)malloc(sizeof(int*) * 1000);
    int* used = (int*)malloc(sizeof(int) * numsSize);
    //将used数组中元素都置0
    initialize(used, numsSize);
    ansTop = pathTop = 0;

    backTracking(nums, numsSize, used);

    //设置path和ans数组的长度
    *returnSize = ansTop;
    *returnColumnSizes = (int*)malloc(sizeof(int) * ansTop);
    int i;
    for(i = 0; i < ansTop; i++) {
        (*returnColumnSizes)[i] = numsSize;
    }
    return ans;
}

13、全排列II

47. 全排列 II - 力扣（LeetCode） (opens new window)

1、题目

• 给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

示例 1：
输入：nums = [1,1,2]
输出：
[[1,1,2],
 [1,2,1],
 [2,1,1]]
    
示例 2：
输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

• 提示：
  • 1 <= nums.length <= 8
  • -10 <= nums[i] <= 10

2、思路

• 这道题目和46.全排列 (opens new window) (opens new window)的区别在与给定一个可包含重复数字的序列，要返回所有不重复的全排列。

• 还要强调的是去重一定要对元素进行排序，这样我们才方便通过相邻的节点来判断是否重复使用了。

• 以示例中的 [1,1,2]为例 （为了方便举例，已经排序）抽象为一棵树，去重过程如图：

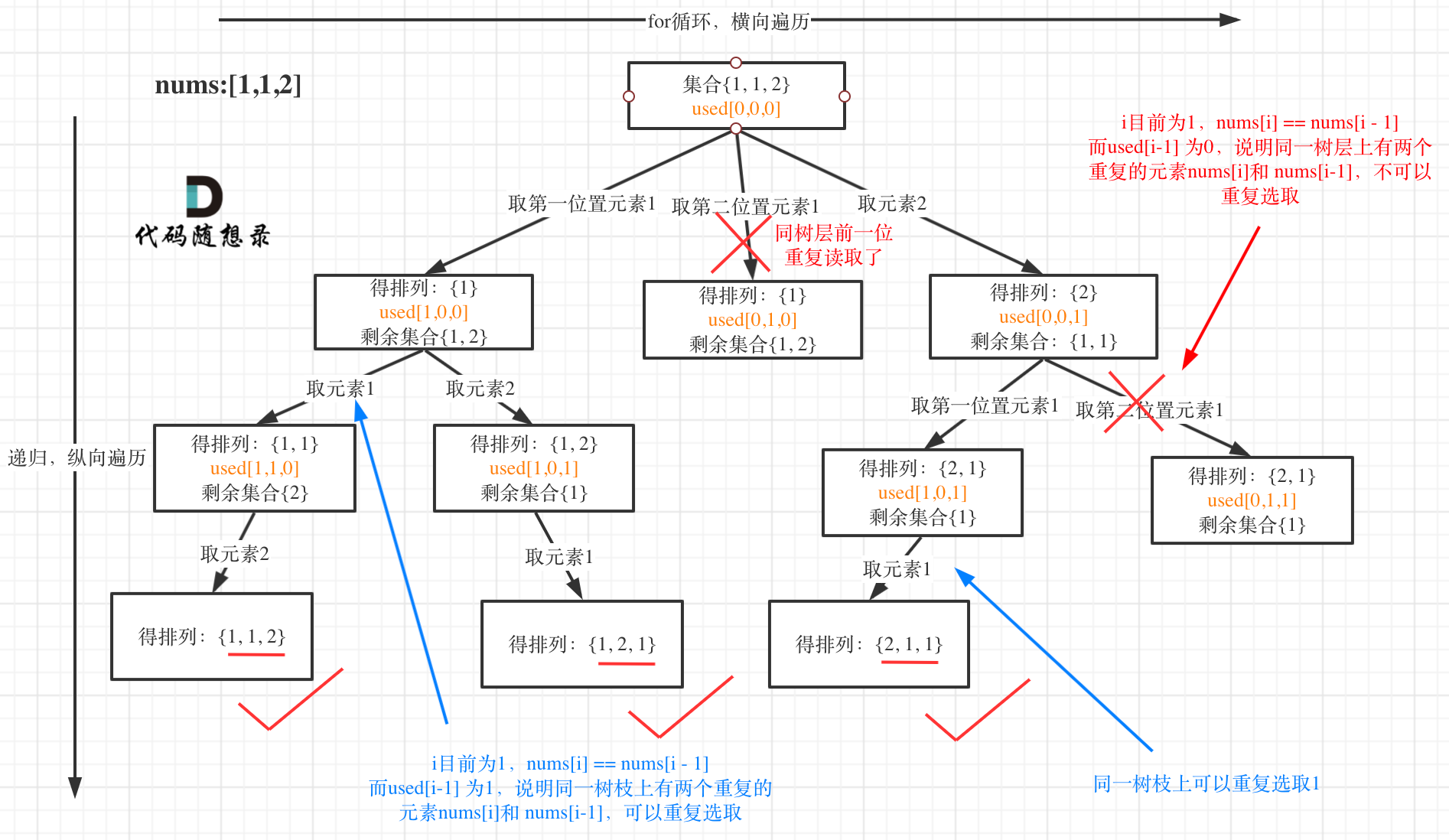
• 图中我们对同一树层，前一位（也就是nums[i-1]）如果使用过，那么就进行去重。

  一般来说：组合问题和排列问题是在树形结构的叶子节点上收集结果，而子集问题就是取树上所有节点的结果。

3、代码

//临时数组
int *path;
//返回数组
int **ans;
int *used;
int pathTop, ansTop;

//拷贝path到ans中
void copyPath() {
    int *tempPath = (int*)malloc(sizeof(int) * pathTop);
    int i;
    for(i = 0; i < pathTop; ++i) {
        tempPath[i] = path[i];
    }
    ans[ansTop++] = tempPath;
}

void backTracking(int* used, int *nums, int numsSize) {
    //若path中元素个数等于numsSize，将path拷贝入ans数组中
    if(pathTop == numsSize)
        copyPath();
    int i;
    for(i = 0; i < numsSize; i++) {
        //若当前元素已被使用
        //或前一位元素与当前元素值相同但并未被使用
        //则跳过此分支
        if(used[i] || (i != 0 && nums[i] == nums[i-1] && used[i-1] == 0))
            continue;

        //将当前元素的使用情况设为True
        used[i] = 1;
        path[pathTop++] = nums[i];
        backTracking(used, nums, numsSize);
        used[i] = 0;
        --pathTop;
    }
}

int cmp(void* elem1, void* elem2) {
    return *((int*)elem1) - *((int*)elem2);
}

int** permuteUnique(int* nums, int numsSize, int* returnSize, int** returnColumnSizes){
    //排序数组
    qsort(nums, numsSize, sizeof(int), cmp);
    //初始化辅助变量
    pathTop = ansTop = 0;
    path = (int*)malloc(sizeof(int) * numsSize);
    ans = (int**)malloc(sizeof(int*) * 1000);
    //初始化used辅助数组
    used = (int*)malloc(sizeof(int) * numsSize);
    int i;
    for(i = 0; i < numsSize; i++) {
        used[i] = 0;
    }

    backTracking(used, nums, numsSize);

    //设置返回的数组的长度
    *returnSize = ansTop;
    *returnColumnSizes = (int*)malloc(sizeof(int) * ansTop);
    int z;
    for(z = 0; z < ansTop; z++) {
        (*returnColumnSizes)[z] = numsSize;
    }
    return ans;
}

4、拓展

• 详见代码随想录 (programmercarl.com) (opens new window)